What is a Quantum System
A quantum system is traditionally defined as an object or a collection of objects in the scale of the electron or of the atoms, the description of which is governed by the laws of quantum mechanics. However, it has become increasingly evident that the grips of quantum mechanics extend much beyond this traditional scale of a quantum object. Recent experiments have shown that the quintessential signature of quantum behavior—self-interference—is not only manifested by electrons and atoms but also by much larger objects such as the fullerene, an arrangement of 60-carbon atoms taking the shape of the soccer ball; and, more recently, large organic molecules that are compounds of 430 atoms. Also it is already known that much more complex systems with internal degrees of freedom more than 1000 manifest self-interference.
These recent experiments, together with the recent theoretical developments of quantum mechanics, point to the conclusion that it is only our technological ability to isolate objects from their environments that stands in the way in their manifesting quantum behavior. The theoretical developments have afforded us the understanding that even the lack of self-interference by larger objects can be explained entirely within the scope of quantum mechanics. All these taken together lead us to the conclusion that quantum mechanics applies to the entire spectrum of spatial sizes and structural complexities. Hence any object or a collection of objects that we can conceive of (say the chair you are sitting on right now) can be legitimately identified as a quantum object, with the full or degraded manifestation of self-interference determined only by the degree the system is isolated from its environment.
So, given a quantum system, how do we proceed in describing it quantum mechanically? Quantum mechanics demands that a quantum object is identified with a complex, separable Hilbert space. In short a quantum system is a Hilbert space in its barest mathematical sense. The Hilbert space description of a quantum object is a natural consequence of the quantum superposition principle, the physical manifestation of which is the well-known self-interference phenomenon. Quantum mechanics as we know it is just the set of rules that relate the different structures of the underlying Hilbert space with outcomes of our measurements on the system. In this post, we will see how the superposition principle, in conjunction with the concept of mutually exclusive outcomes, leads to the construction of the Hilbert space of a quantum system.
The Quantum Hilbert Space
Central to the description of any physical system is the concept of state of a system. The state is the collection of minimal information that completely describes the system at a given moment. It encodes all the information that we can ever extract from the system. It is the initial data fed into the formal rules of the appropriate physics that yields predictions into the outcomes of measurements made on the system. The collection of all possible states constitutes the state space of the system. For example, for a classical particle, the collection of position and momentum of the particle at any instant of time constitute the state of the particle at that instant; the initial position and momentum—the initial state—fed into Newton’s laws of motion predicts all outcomes of measurements made on the particle. The volume of the phase space available to the particle constitutes its state space.
Now the state space of a quantum system splits in two in accordance with the predictability of outcomes of measurements on the system. A state is referred to as a pure state if there exists a measurement whose outcome is completely predictable when the system is prepared in that state. Otherwise, the state is referred to as a mixed state if there exists no measurement whose outcome is predictable when the system is prepared in that state. Mixed states are expressible in terms of pure states (some statistical averages of pure states) so that pure states lay at the foundation of the state space of a quantum system. Quantum mechanics postulates that pure states of a quantum system constitute a complex, separable Hilbert space. Constructing or assigning the Hilbert space of a quantum system is identifying all possible pure states of the system, through them the whole state space of the system is constituted.
A Hilbert space has two basic constituents: its dimension and its inner product. Once these two are specified the corresponding unique (up to a unitary transformation) Hilbert space can already be constructed. Quantum mechanics provides the recipe of identifying the dimension and the inner product; the recipe is based on measurements of observables of the system under consideration. Now an observable is any measurable property of the system, such as energy and momentum. Without losing generality, we will only consider discrete observables in this post. Not all possible observables of the system may serve to define the Hilbert space. The observables that are relevant to the construction of the Hilbert space are known as sharp observables, in contrast to the non-relevant ones known as unsharp observables. We will have a separate posting on unsharp observables later.
Let us consider some observable ![]() whose only measurable values are
whose only measurable values are ![]() . The number of measurable values may be finite or infinite. The observable
. The number of measurable values may be finite or infinite. The observable ![]() is a sharp observable if it has the following property: Successive measurements of
is a sharp observable if it has the following property: Successive measurements of ![]() always yield the same value, say
always yield the same value, say ![]() . Successive here means a series of measurements made just right after another measurement. The outcomes of the measurement of
. Successive here means a series of measurements made just right after another measurement. The outcomes of the measurement of ![]() are then said to be mutually exclusive. That is if the result of the measurement is
are then said to be mutually exclusive. That is if the result of the measurement is ![]() , then a measurement made right after
, then a measurement made right after ![]() is obtained excludes all other possible outcomes except
is obtained excludes all other possible outcomes except ![]() itself. For an unsharp observable, there is a chance that the outcome of succession of measurements is different from the first outcome.
itself. For an unsharp observable, there is a chance that the outcome of succession of measurements is different from the first outcome.
We can now proceed with the recipe in discovering the dimension of the system Hilbert space. Let ![]() comprise all possible sharp observables of the given system. Now measure
comprise all possible sharp observables of the given system. Now measure ![]() an arbitrary number of times, with the system in arbitrary configuration each time, and determine the number of possible outcomes of the measurement, say
an arbitrary number of times, with the system in arbitrary configuration each time, and determine the number of possible outcomes of the measurement, say ![]() . Next measure
. Next measure ![]() using the same algorithm, obtaining in the process
using the same algorithm, obtaining in the process ![]() possible outcomes, and so on. Note that the actual value measured is not important here. It is the number of distinct outcomes of measurements that is required. The maximum of the set
possible outcomes, and so on. Note that the actual value measured is not important here. It is the number of distinct outcomes of measurements that is required. The maximum of the set ![]() is the dimension of the system Hilbert space. If the dimension is finite, the system is called a finite dimensional quantum system; otherwise, it is called infinite dimensional.
is the dimension of the system Hilbert space. If the dimension is finite, the system is called a finite dimensional quantum system; otherwise, it is called infinite dimensional.
Finite Dimensional Quantum Systems
Now let ![]() be the Hilbert space of the system which is yet to be specified, except that we presuppose to have already discovered the dimension
be the Hilbert space of the system which is yet to be specified, except that we presuppose to have already discovered the dimension ![]() of
of ![]() . Consider now a sharp observable
. Consider now a sharp observable ![]() whose number of mutually exclusive values equals that of the dimension
whose number of mutually exclusive values equals that of the dimension ![]() of
of ![]() ,
, ![]() ; the values may be arranged in increasing order. Quantum mechanics postulates that to each of the outcome
; the values may be arranged in increasing order. Quantum mechanics postulates that to each of the outcome ![]() corresponds to a pure state
corresponds to a pure state ![]() of the system, with the
of the system, with the ![]() ‘s belonging to the system Hilbert space
‘s belonging to the system Hilbert space ![]() . The correspondence is that if the system is prepared in
. The correspondence is that if the system is prepared in ![]() and
and ![]() is measured thereafter the outcome of the measurement is invariably
is measured thereafter the outcome of the measurement is invariably ![]() . The outcomes
. The outcomes ![]() are mutually exclusive so that the corresponding pure states
are mutually exclusive so that the corresponding pure states ![]() have the property of being a set of mutually exclusive states. This property means that if the system is prepared in the state
have the property of being a set of mutually exclusive states. This property means that if the system is prepared in the state ![]() then measurement of
then measurement of ![]() excludes the possibility of obtaining an outcome corresponding to
excludes the possibility of obtaining an outcome corresponding to ![]() for
for ![]() .
.
Let ![]() be the inner product of the Hilbert space
be the inner product of the Hilbert space ![]() , which until here is unspecified. Quantum mechanics postulates that the mutual exclusivity of the states
, which until here is unspecified. Quantum mechanics postulates that the mutual exclusivity of the states ![]() translates to the statement that the set is an orthogonal set. Explicitly
translates to the statement that the set is an orthogonal set. Explicitly
(1) ![]()
Without sacrificing generality, we can always assume that the ![]() ‘s are normalized, i.e.
‘s are normalized, i.e. ![]() or
or ![]() . Then the set
. Then the set ![]() is an orthonormal set, i.e.
is an orthonormal set, i.e. ![]() . We can now restate the principle
. We can now restate the principle
(2) ![]()
That is a set of mutually exclusive pure states is an orthonormal set.
The entire vector space of pure states is constructed using the quantum superposition principle which states that there exists a meaningful operation of addition ![]() of pure states and multiplication
of pure states and multiplication ![]() of complex numbers and pure states such that the linear sum
of complex numbers and pure states such that the linear sum ![]() is again a pure state of the system for every pure states
is again a pure state of the system for every pure states ![]() ,
, ![]() and complex numbers
and complex numbers ![]() ,
, ![]() . Using this principle, quantum mechanics demands that the mutually exclusive states
. Using this principle, quantum mechanics demands that the mutually exclusive states ![]() form an orthonormal basis of the system Hilbert space
form an orthonormal basis of the system Hilbert space ![]() . Then every pure state
. Then every pure state ![]() or vector of
or vector of ![]() can be written in terms of this basis
can be written in terms of this basis
(3) 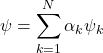
for some complex ![]() ‘s. Notice that the vector
‘s. Notice that the vector ![]() is uniquely identified with the
is uniquely identified with the ![]() -tuple of complex numbers
-tuple of complex numbers ![]() .
.
Finally we are in the position to identify the inner product of the Hilbert space ![]() . Given an arbitrary pair of of vectors
. Given an arbitrary pair of of vectors
(4) 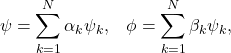
their inner product is deduced from the orthonormality of the basis vectors using the linear and antilinear properties of the inner product. We arrive at the inner product
(5) 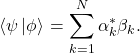
Again notice that the resulting inner product depends only on the ![]() -tuple of complex numbers identifying the vectors. Finally we obtain that the Hilbert space of an
-tuple of complex numbers identifying the vectors. Finally we obtain that the Hilbert space of an ![]() -dimensional quantum system is
-dimensional quantum system is ![]() .
.
The foregoing is an abstract description of the Hilbert space of a finite dimensional Hilbert space. The Hilbert space is made concrete and practicable by an explicit representation of the pure states in terms of column matrices. This is possible because matrices of fixed sizes form a vector space and the inner product can be implemented in terms of a known matrix operation.
To simplify our notation let us just consider the simplest quantum system, the qubit which is a two dimensional quantum system with the Hilbert space ![]() . Vectors in
. Vectors in ![]() are uniquely identified with a 2-tuple of complex numbers
are uniquely identified with a 2-tuple of complex numbers ![]() , and they can be represented as
, and they can be represented as ![]() column vectors,
column vectors,
(6) ![]()
The vector space structure of ![]() is implemented with the usual rules of matrix operations. In particular, for arbitrary complex numbers
is implemented with the usual rules of matrix operations. In particular, for arbitrary complex numbers ![]() and vectors
and vectors ![]() we have
we have
(7) ![]()
On the other hand the inner product is implemented by means of the multiplication of matrices,
(8) ![]()
All these taken together we identify the basis vectors, representing a particular set of mutually exclusive states, are given by
(9) ![]()
Of course, these are not the only possible basis vectors; there are, in fact, infinitely many of them. This means that the underlying quantum system has an infinitely many sharp observables.
The extension of the column vector representation of ![]() for arbitrary positive integer
for arbitrary positive integer ![]() is evident.
is evident.
Infinite Dimensional Quantum Systems
For infinite dimensional quantum systems, there are subtle issues that arise in the construction of the Hilbert space. The problem lies in the possibility that a given measurable value corresponds to more than one distinct configuration or state of the system. This can be avoided by constructing a basis out of an observable of the system that has infinite number of possible values with the property that to every value there corresponds one and only one configuration or state of the system that yields the same value. Such an observable is known as a non-degenerate observable; otherwise, it is known as degenerate. Once such an observable has been identified, we can proceed in a similar fashion as in the case of finite dimensional systems except that one has to go via the pre-Hilbert space and then followed by completion of the pre-Hilbert space to obtain the Hilbert space. This leads us to the Hilbert space ![]() for an infinite dimensional quantum system. We will have a separate posting to elaborate the infinite dimensional case.
for an infinite dimensional quantum system. We will have a separate posting to elaborate the infinite dimensional case.