Introduction
A system is an object or a collection of objects whose properties are subject to observation and measurement. The state of a given system is the minimum collection of information that completely describes the system. For a classical particle, its state is specified by giving its position and momentum at any given time. The state space of the particle is the two-dimensional phase-space of position and momentum, every point in which describes a state of the particle. On the other hand, the state of a quantum object, such as an atom, is described not in terms of position and momentum but of complex-valued functions that comprise the state space of the quantum object. The state space of a quantum object has the structure of a complex, separable Hilbert space. To describe a quantum object one needs to specify the Hilbert space that is uniquely associated with the system. Here I describe the Hilbert space that is relevant to quantum mechanics.
Vector Space
A complex vector space is a set ![]() , together with a rule that defines the sum (denoted by
, together with a rule that defines the sum (denoted by ![]() ) of elements of
) of elements of ![]() and a rule that defines the product (denoted by
and a rule that defines the product (denoted by ![]() ) of any complex number and any element of
) of any complex number and any element of ![]() . The sum and the product satisfy the following axioms: For every complex numbers
. The sum and the product satisfy the following axioms: For every complex numbers ![]() and elements
and elements ![]() in
in ![]() ,
,
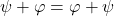 belongs to
belongs to 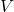 ,
,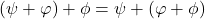 ,
,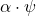 belongs to
belongs to 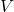 ,
,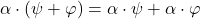
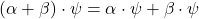
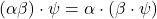
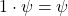
- There exists a unique element
 of
of  such that for all
such that for all  in
in  the equality
the equality 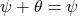 holds.
holds. - To every element
 of
of 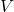 there exists a unique element
there exists a unique element 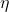 of
of 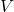 such that
such that 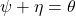 . The element
. The element 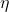 is given by
is given by 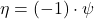 , which we denote simply by
, which we denote simply by 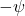 .
.
The ordered triplet ![]() constitutes a complex vector space, and the elements of
constitutes a complex vector space, and the elements of ![]() are called vectors. More than one pair of rules
are called vectors. More than one pair of rules ![]() can be assigned to the given set
can be assigned to the given set ![]() , with each pair defining a distinct vector space with
, with each pair defining a distinct vector space with ![]() . If the pair
. If the pair![]() is clear from the outset, the set
is clear from the outset, the set ![]() can be simply referred to as a vector space.
can be simply referred to as a vector space.
Example-1. Let ![]() denote the set of all
denote the set of all ![]() -tuple complex numbers. A typical element
-tuple complex numbers. A typical element ![]() of this set is given by
of this set is given by ![]() where the
where the ![]() ‘s are arbitrary complex numbers. On its own,
‘s are arbitrary complex numbers. On its own, ![]() is just a set and not a vector space. It is turned into a vector space by defining the sum of every pair of its elements, and defining the product of its every vector with a complex number that satisfy the above axioms of a vector space. Given two arbitrary elements
is just a set and not a vector space. It is turned into a vector space by defining the sum of every pair of its elements, and defining the product of its every vector with a complex number that satisfy the above axioms of a vector space. Given two arbitrary elements ![]() and
and ![]() of
of ![]() , we define their sum to be
, we define their sum to be ![]() , where
, where ![]() , for all
, for all ![]() , denote the usual addition of complex numbers. Moreover, we define the product of any element
, denote the usual addition of complex numbers. Moreover, we define the product of any element ![]() and complex number
and complex number ![]() to be
to be ![]() , where
, where ![]() denote the usual multiplication of complex numbers.
denote the usual multiplication of complex numbers.
Using the known properties of complex numbers, it is not difficult to show that all the axioms 1 to 7 of a vector space are satisfied by these definitions. Now the ![]() -tuple of zeros,
-tuple of zeros, ![]() , belongs to
, belongs to
![]() , the numeric zero being a complex number itself; moreover,
, the numeric zero being a complex number itself; moreover, ![]() satisfies
satisfies ![]() for all
for all ![]() . Hence
. Hence ![]() is the zero of
is the zero of ![]() with respect to the given sum. From this, for every
with respect to the given sum. From this, for every ![]() we can find a
we can find a ![]() in
in ![]() such that
such that ![]() ; it is given by
; it is given by ![]() .Then
.Then ![]() , together with the defined sum and multiplication, is a complex vector space.
, together with the defined sum and multiplication, is a complex vector space. ![]()
Example-2. Let ![]() denote the set of all continuous, complex valued, (Lebesque) square integrable functions
denote the set of all continuous, complex valued, (Lebesque) square integrable functions ![]() in the real line
in the real line ![]() ; the last property of the elements of the set means
; the last property of the elements of the set means ![]() . The function
. The function ![]() for all real
for all real ![]() (the function that identically vanishes in the entire real line) belongs to this set. The set
(the function that identically vanishes in the entire real line) belongs to this set. The set ![]() is a vector space under the usual rule of pointwise addition of functions and the usual rule of multiplication of complex numbers with any complex valued function. That is if
is a vector space under the usual rule of pointwise addition of functions and the usual rule of multiplication of complex numbers with any complex valued function. That is if ![]() and
and ![]() belong to this set, then their sum is defined to be the function
belong to this set, then their sum is defined to be the function ![]() , where the plus sign indicate the usual addition of complex numbers.
, where the plus sign indicate the usual addition of complex numbers.
The sum belongs to the set again. This follows from the well-known inequality, ![]() . Since the two terms in the right hand of the side are both finite, the left hand side must be finite, too. That is
. Since the two terms in the right hand of the side are both finite, the left hand side must be finite, too. That is ![]() is itself square integrable. Also for any complex
is itself square integrable. Also for any complex ![]() and function
and function ![]() in
in ![]() , the function
, the function ![]() is clearly in the set, too. Finally the zero vector of the set is
is clearly in the set, too. Finally the zero vector of the set is ![]() . The rest of the axioms of a vector space can be easily shown to be satisfied.
. The rest of the axioms of a vector space can be easily shown to be satisfied. ![]()
Inner Product Space
A complex inner product space is a complex vector space ![]() together with a binary operation
together with a binary operation ![]() taking pairs of vectors of
taking pairs of vectors of ![]() into complex numbers such that for every complex
into complex numbers such that for every complex
numbers ![]() ,
, ![]() and vectors
and vectors ![]() ,
, ![]() ,
, ![]() in
in ![]() the following axioms are satisfied:
the following axioms are satisfied:
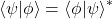 ,
,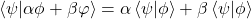 ,
,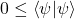 , with
, with 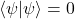 if and only if
if and only if  is the zero vector.
is the zero vector.
The ordered pair ![]() constitutes an inner product space. If from the outset the inner product is clear, the set
constitutes an inner product space. If from the outset the inner product is clear, the set ![]() can be referred to as an inner product space.
can be referred to as an inner product space.
Example-1. For the vector space ![]() , the following inner product can be introduced: For every pair of vectors
, the following inner product can be introduced: For every pair of vectors ![]() and
and ![]() , define
, define
(1) 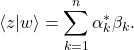
It is not difficult to show that this binary operation satisfies all the properties of an inner product.![]()
Example-2. For the vector space ![]() , the following inner product can be introduced: For every pair of vectors
, the following inner product can be introduced: For every pair of vectors ![]() and
and ![]() , define
, define
(2) ![]()
From the linear property of the integral, it can shown that this binary operation satisfies all the axioms of an inner product.![]() .
.
Then ![]() and
and ![]() , together with their respective inner products defined above, are inner product spaces.
, together with their respective inner products defined above, are inner product spaces.
Normed Space
A complex normed space is a complex vector space ![]() together with an operation
together with an operation ![]() taking vectors of
taking vectors of ![]() such that for every complex number
such that for every complex number ![]() and vectors
and vectors ![]() ,
, ![]() in
in ![]() the following axioms are satisfied:
the following axioms are satisfied:
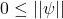 , with
, with 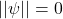 if and only if
if and only if  is the zero vector,
is the zero vector,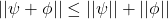 ,
,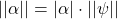 .
.
The ordered pair ![]() is called a complex normed space. The positive number
is called a complex normed space. The positive number ![]() is called the norm of the vector
is called the norm of the vector ![]() . The norm is a generalization of the concept of length in an abstract set. An inner product space can be turned into a normed space by equipping the vector space with the norm
. The norm is a generalization of the concept of length in an abstract set. An inner product space can be turned into a normed space by equipping the vector space with the norm ![]() .
.
Example-1. The inner product space ![]() is a normed space under the norm induced by the inner product \eqref{c1}. The norm is given by
is a normed space under the norm induced by the inner product \eqref{c1}. The norm is given by
(3) 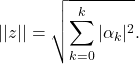
. ![]()
Example-2. The inner product space ![]() is a normed space under the norm induced by the inner product \eqref{c2}. The norm is given by
is a normed space under the norm induced by the inner product \eqref{c2}. The norm is given by
(4) 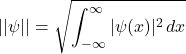
. ![]()
Metric Space
A complex metric space is a complex vector space ![]() together with a binary operation
together with a binary operation ![]() such that for every vectors
such that for every vectors ![]() ,
, ![]() ,
, ![]() in
in ![]() the following axioms are satisfied:
the following axioms are satisfied:
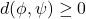 , with
, with 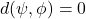 if and only if
if and only if 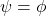 ,
,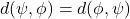 ,
,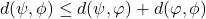 .
.
The ordered set ![]() constitute a metric space. The metric is a generalization of the concept of distance between two points. Observe that an normed space can be made into a metric space by defining the metric as
constitute a metric space. The metric is a generalization of the concept of distance between two points. Observe that an normed space can be made into a metric space by defining the metric as ![]() . A metric defines equality of vectors, i.e. two vectors are equal if the distance between them is zero, even though they are not identical. (This point will be illustrated below.) Also a metric defines the convergence of a sequence of vectors in
. A metric defines equality of vectors, i.e. two vectors are equal if the distance between them is zero, even though they are not identical. (This point will be illustrated below.) Also a metric defines the convergence of a sequence of vectors in ![]() to a particular vector in
to a particular vector in ![]() .
.
Example-1. The inner product space ![]() is a metric space under the metric induced by the norm \eqref{d1}. The metric is given by
is a metric space under the metric induced by the norm \eqref{d1}. The metric is given by
(5) 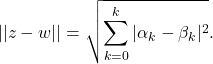
. ![]()
Example-2. The inner product space ![]() is a metric space under the metric induced by the norm \eqref{d2}. The metric is given by
is a metric space under the metric induced by the norm \eqref{d2}. The metric is given by
(6) 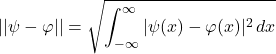
![]()
Hilbert Space
A complex pre-Hilbert space ![]() is a complex linear vector space equipped with an inner product
is a complex linear vector space equipped with an inner product ![]() , with a norm given by
, with a norm given by ![]() , and with a metric
, and with a metric ![]() . Thus to define a pre-Hilbert space one only needs to specify the vector space involved and to define the corresponding inner product. Note that a given vector space maybe equipped with more than one inner product. In quantum mechanics the choice of inner product is not arbitrary but dictated by physical considerations.
. Thus to define a pre-Hilbert space one only needs to specify the vector space involved and to define the corresponding inner product. Note that a given vector space maybe equipped with more than one inner product. In quantum mechanics the choice of inner product is not arbitrary but dictated by physical considerations.
Before we can define what is a Hilbert space, we need the concept of a Cauchy sequence. A sequence of vectors in a pre-Hilbert space ![]() is an indexed collection of vectors, i.e.
is an indexed collection of vectors, i.e. ![]() with each
with each ![]() belonging to
belonging to ![]() . A sequence is called Cauchy if
. A sequence is called Cauchy if ![]() . The pre-Hilbert space
. The pre-Hilbert space ![]() is called complete if for every Cauchy sequence
is called complete if for every Cauchy sequence ![]() in
in ![]() there exists a vector
there exists a vector ![]() in
in ![]() such that
such that ![]() .
.
A complete pre-Hilbert space is called a Hilbert space.
A pre-Hilbert space which is not complete can be turned into a Hilbert space by adding all limits of Cauchy sequences to the pre-Hilbert space itself. The resulting Hilbert space is called the completion or closure of the pre-Hilbert space. Generally, Hilbert spaces are constructed in this way. That is one starts with a linear space, then equips that space with an inner product to make it into a pre-Hilbert space, then finally completes the pre-Hilbert space to get a Hilbert space.
Example-1. ![]() , together with the inner product \eqref{c1}, is a pre-Hilbert space which is already a Hilbert space.
, together with the inner product \eqref{c1}, is a pre-Hilbert space which is already a Hilbert space. ![]()
Example-2. ![]() , together with the inner product \eqref{c2}, is a pre-Hilbert space which is not a Hilbert space. The reason is that there are Cauchy sequences in the vector space which do not converge to continuous functions. For example, the sequence of continuous functions given by
, together with the inner product \eqref{c2}, is a pre-Hilbert space which is not a Hilbert space. The reason is that there are Cauchy sequences in the vector space which do not converge to continuous functions. For example, the sequence of continuous functions given by
(7) 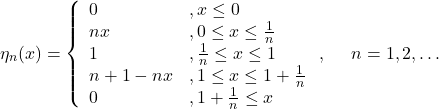
is a Cauchy sequence in ![]() . However, the sequence converges to the function which has the value
. However, the sequence converges to the function which has the value ![]() in the interval
in the interval ![]() and
and ![]() elsewhere, which is clearly not continuous but belonging to
elsewhere, which is clearly not continuous but belonging to ![]() . The pre-Hilbert space is then not complete. To construct a Hilbert space out of
. The pre-Hilbert space is then not complete. To construct a Hilbert space out of![]() , we adjoin to
, we adjoin to ![]() all limits of its Cauchy sequences. The resulting Hilbert space then consists not only continuous functions but also non-continuous functions. The Hilbert space is denoted by
all limits of its Cauchy sequences. The resulting Hilbert space then consists not only continuous functions but also non-continuous functions. The Hilbert space is denoted by ![]()
A peculiarity of ![]() is that its vectors are not individual functions but classes of functions. Consider the function
is that its vectors are not individual functions but classes of functions. Consider the function ![]() , which, of course, belongs to
, which, of course, belongs to![]() . Now define the function
. Now define the function ![]() for all
for all ![]() and
and ![]() for
for ![]() . While
. While ![]() is infinite at
is infinite at ![]() , the integral
, the integral ![]() exists, and in fact its value is given by
exists, and in fact its value is given by ![]() . That is so because the value of an integral does not change by changing the value of the integrand at isolated points. Thus
. That is so because the value of an integral does not change by changing the value of the integrand at isolated points. Thus ![]() is a vector of
is a vector of ![]() . Now
. Now ![]() for all
for all ![]() , so that
, so that ![]() or
or ![]() . By the definition of equality of vectors of a metric space, the functions
. By the definition of equality of vectors of a metric space, the functions ![]() and
and ![]() , while they are not equal pointwise, represent the same vector in
, while they are not equal pointwise, represent the same vector in![]() . Also we can introduce the new function
. Also we can introduce the new function ![]() for all
for all ![]() , with
, with ![]() , and assign arbitrary values to
, and assign arbitrary values to ![]() at
at ![]() and
and ![]() . Again
. Again ![]() are not equal pointwise, but
are not equal pointwise, but ![]() ,
, ![]() ,
, ![]() so that they represent the same vector in
so that they represent the same vector in ![]() . Clearly we can go on changing the values of
. Clearly we can go on changing the values of ![]() at isolated points to obtain an infinite number of functions that differ with
at isolated points to obtain an infinite number of functions that differ with ![]() at isolated points only but with zero distance with
at isolated points only but with zero distance with ![]() . We can now see that a class of functions represents a vector of
. We can now see that a class of functions represents a vector of![]() .
. ![]()
Separable Hilbert Spaces
Some collection of vectors, ![]() , of a Hilbert space
, of a Hilbert space ![]() is called linearly independent if the sum
is called linearly independent if the sum
(8) ![]()
implies that ![]() . The largest number of linearly independent vectors in a Hilbert space is the dimension
. The largest number of linearly independent vectors in a Hilbert space is the dimension ![]() of the Hilbert space. If
of the Hilbert space. If ![]() is finite, the Hilbert space is finite dimensional; otherwise, it is infinite dimensional. A Hilbert space
is finite, the Hilbert space is finite dimensional; otherwise, it is infinite dimensional. A Hilbert space ![]() is called separable if there exists a set of linearly independent vectors in
is called separable if there exists a set of linearly independent vectors in ![]() ,
, ![]() , such that for every vector
, such that for every vector ![]() in
in ![]() there exists a set of complex numbers
there exists a set of complex numbers ![]() such that
such that
(9) ![]()
The number of such independent vectors must necessarily equal the dimensionality of the the Hilbert space. When such set satisfies the condition, the set is said to span the Hilbert space. Not all Hilbert spaces are separable. The Hilbert space of quantum mechanics is separable; because of that whenever we refer to a Hilbert space from hereon we mean separable Hilbert space.
Two vectors ![]() and
and ![]() are called orthogonal if
are called orthogonal if ![]() . A set of independent vectors, which we denote shorthand by
. A set of independent vectors, which we denote shorthand by ![]() , is called an orthogonal set if
, is called an orthogonal set if ![]() when
when ![]() . Moreover, the set is called an orthonormal set if
. Moreover, the set is called an orthonormal set if ![]() where
where ![]() is the Kronecher delta function,
is the Kronecher delta function, ![]() and
and ![]() . When the set
. When the set ![]() spans the Hilbert space, the set is called an orthonormal basis for the Hilbert space
spans the Hilbert space, the set is called an orthonormal basis for the Hilbert space ![]() . Thus when
. Thus when ![]() is an orthonormal basis, every vector
is an orthonormal basis, every vector ![]() in
in ![]() can be written as the sum given by equation-\eqref{vectorsum}. The coefficients
can be written as the sum given by equation-\eqref{vectorsum}. The coefficients ![]() are found using the orthonormality of the
are found using the orthonormality of the ![]() ‘s and the linearity of the inner product,
‘s and the linearity of the inner product,
(10) 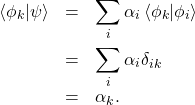
Hence the coefficients are given by ![]() . The
. The ![]() ‘s are called the Fourier coefficients of
‘s are called the Fourier coefficients of ![]() with respect to the basis set
with respect to the basis set ![]() . From this definition it is clear that a given set of orthonormal vectors form a basis if and only if
. From this definition it is clear that a given set of orthonormal vectors form a basis if and only if ![]() for all
for all ![]() implies that
implies that ![]() .
.