Beauty is one of those abstractions that is difficult to define or quantify. But we know it when we see one. I arrived at the following integral trying to make sense of some divergent integrals:
(1) ![]()
There is manifest symmetry in the integrand and the value of the integral involves the ratio of two of the most ubiquitous math constants.
I think it’s beautiful.
It is untabulated as of its posting (as far as I’m aware), and unimplemented in Mathematica 10.2 and Maple 18.0 (anyone with Maple 2015?). Try if you can arrive at it, too. Feel free to post your solution below.
Stunning result. Any hint as to the methods involved?
The integral can be obtained by performing the contour integration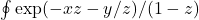 along the quarter circle in the first quadrant of the complex plane, integrating through simple poles via the principal value.
along the quarter circle in the first quadrant of the complex plane, integrating through simple poles via the principal value.