This blogpost is aimed to explain some portions of our paper “Dissipative preparation of phase and number squeezed states using ultracold atoms” (Phys. Rev. A 89, 013620 (2014)), authored by Gentaro Watanabe, Harri Makela, Sebastian Diehl, Markus Oberthaler and myself. At the time of the collaboration, Prof. Watanabe was based at the Asia Pacific Center for Theoretical Physics in Pohang, Republic of Korea, where I was doing my postdoctoral research while on leave from the National Institute of Physics, UP Diliman; Dr. Makela was based at Aalto University in Finland; Prof. Diehl was based at the University of Innsbruck in Austria and Prof. Oberthaler was based at the University of Heidelberg in Germany. It is of interest to note that all of the authors were never in one place simultaneously to work on the paper; rather, the collaboration for this paper began with Prof. Watanabe and Dr. Makela, and grew to include Prof. Diehl and myself, and finally included Prof. Oberthaler afterwards. Prof. Watanabe and Dr. Makela, as well as Prof. Watanabe and myself, worked together in person on the paper, while Prof. Diehl sent in his contributions by email and Skype, and Prof. Oberthaler sent his by email. As can be seen, only two or three authors at a time were interacting face to face in this collaboration. This illustrates the role of technology in carrying out scientific collaborations, and highlights the fact that collaborators need not be at the same place at the same time to do scientific work.
The paper focuses on the preparation of a specific type of squeezed quantum state by dissipative processes, namely phase and number squeezed quantum states. A squeezed state is a quantum state for which the lower bound of the quantum uncertainty principle holds, i. e.,
(1) ![]()
where ![]() and
and ![]() are quantum observables that satisfy the commutation relation
are quantum observables that satisfy the commutation relation ![]() , such as position and momentum, or phase and particle number. This then implies that for the equality to hold, the uncertainty of one of the observables, say
, such as position and momentum, or phase and particle number. This then implies that for the equality to hold, the uncertainty of one of the observables, say ![]() , is minimized, while the uncertainty
, is minimized, while the uncertainty ![]() is maximized, or vice versa. This is an acceptable consequence since the minimal uncertainty of
is maximized, or vice versa. This is an acceptable consequence since the minimal uncertainty of ![]() for this squeezed states enables one to use it in experiments which require high precision in
for this squeezed states enables one to use it in experiments which require high precision in ![]() .
.
Now for phase and number squeezed states, one possible application would be in atom interferometry experiments. One requirement of such experiments is the detection of a specific population, or number, of atoms in the state. If one is able to do this, then the relative phase of the state’s wavefunction components can be determined from the interference fringes. Now from the uncertainty principle, we can minimize the uncertainty in the relative phase of the state’s wavefunction components, but if we want to minimize the total uncertainty, then we must maximize the uncertainty in the number of atoms present in the state. In other words, for the smallest possible uncertainty in the relative phase of the wavefunction’s components for the system, we must use a phase squeezed state. Similarly, in experiments requiring minimal uncertainty in the number of atoms present in the system, we must use a number squeezed state, since this state has minimal uncertainty in its particle number while having maximal uncertainty in the overall phase of the system.
To be able to prepare a squeezed state that will be used in an atom interferometry experiment, we can take an ensemble of atoms, evolve them unitarily over time, then conduct a series of measurements on them, with the squeezed state emerging as a result of these measurements. However, such a process is laborious due to the series of measurements being carried out; the errors due to these measurements to prepare the state can pile up, and as a consequence the resulting state may not be a squeezed state at all. However, there is an alternative to this process that allows us to minimize the involvement of experimenters in the preparation of the state and at the same time minimize measurement errors that will destroy the squeezedness of the state. This process is a dissipative quantum state preparation process; in it, we create a quantum bath, couple it to a system, and the interaction between the bath and the system will drive the system towards the state that we want to prepare.
The advantage of a dissipative quantum state preparation process is that first, this minimizes experimental errors in the preparation of the state, since it is the interaction between system and environment that drives the system towards the target state; and second, the process is independent of the system to which the bath is coupled. We can use any initial state for our system coupled to the bath, and the resulting prepared state will be the same. However, the process is dependent first on the bath prepared, and second on whether or not there exists a steady state for the equations describing the dynamics of the combined system and bath. However, it may be much easier to prepare the bath than to prepare the state by a series of measurements, which makes dissipative quantum state preparation much more attractive.
We then consider a dissipative quantum state preparation scheme to prepare phase and number squeezed states. To formulate such a scheme, we must first describe the system to be used to prepare such states. In this case, our system is an ultracold atom gas in a trapping potential, which is coupled to a BEC which acts as a bath. The trapping potential has the form of a double well potential embedded in a wide harmonic oscillator potential (for a pictorial representation of the set up, please see the paper itself). To describe it, the state is initially in one of the two double wells located at nodes 1 or 2 with energy level ![]() and energy eigenstates
and energy eigenstates ![]() and
and ![]() corresponding to nodes 1 and 2, respectively and corresponding. Using a Raman laser, these ground states are then coupled to one of two energy levels
corresponding to nodes 1 and 2, respectively and corresponding. Using a Raman laser, these ground states are then coupled to one of two energy levels ![]() or
or ![]() in the harmonic potential, with corresponding energy eigenstates
in the harmonic potential, with corresponding energy eigenstates ![]() and
and ![]() respectively. In particular, the ground states with wavefunctions
respectively. In particular, the ground states with wavefunctions ![]() and
and ![]() are coupled to the energy state
are coupled to the energy state ![]() using Raman lasers with Rabi frequencies
using Raman lasers with Rabi frequencies ![]() and
and ![]() respectively, and the ground states with wavefunctions
respectively, and the ground states with wavefunctions ![]() and
and ![]() are coupled to the energy state
are coupled to the energy state ![]() using Raman lasers with equal Rabi frequencies
using Raman lasers with equal Rabi frequencies ![]() . Due to the coupling between this system and the BEC bath, the system in one of the two excited states
. Due to the coupling between this system and the BEC bath, the system in one of the two excited states ![]() and
and ![]() will then decay back to one of the ground states
will then decay back to one of the ground states ![]() or
or ![]() by emission of a phonon into the BEC with energy
by emission of a phonon into the BEC with energy ![]() . The BEC then absorbs the phonon emitted as the atoms decay back to the ground state.
. The BEC then absorbs the phonon emitted as the atoms decay back to the ground state.
Now we need to formulate the Hamiltonians describing the system, the bath and the interaction between the system and the bath. Their respective Hamiltonians will then have the following form:
(2) 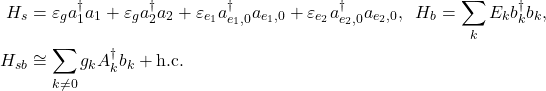
Here, ![]() is the annihilation operator corresponding to energy level
is the annihilation operator corresponding to energy level ![]() ,
, ![]() and
and ![]() is the annihilation operator for the BEC which acts as a bath to which the system is coupled. The operator
is the annihilation operator for the BEC which acts as a bath to which the system is coupled. The operator ![]() describes the transition of the atom from the excited state in the harmonic oscillator to the ground state in the well due to the interaction between an atom and a Bogoliubov excitation coming from the condensate. Explicitly, it has the form
describes the transition of the atom from the excited state in the harmonic oscillator to the ground state in the well due to the interaction between an atom and a Bogoliubov excitation coming from the condensate. Explicitly, it has the form ![]() , where
, where ![]() are the energy eigenfunctions corresponding to energy level
are the energy eigenfunctions corresponding to energy level ![]() at spatial location
at spatial location ![]() ,
, ![]() and
and ![]() .
. ![]() and
and ![]() are the wavenumbers corresponding to the
are the wavenumbers corresponding to the ![]() direction and the transverse directions, respectively, and
direction and the transverse directions, respectively, and ![]() is the trap length in the transverse direction. We note that we evaluate the overlap integral
is the trap length in the transverse direction. We note that we evaluate the overlap integral ![]() only for the transitions
only for the transitions ![]() ,
, ![]() and vice versa, corresponding to transitions of the system from the ground to the excited states and vice versa. On the other hand, the coefficients
and vice versa, corresponding to transitions of the system from the ground to the excited states and vice versa. On the other hand, the coefficients ![]() have the form
have the form
(3) ![]()
where ![]() is the interatomic species scattering length between the atoms trapped in the potential and the atoms in the condensate,
is the interatomic species scattering length between the atoms trapped in the potential and the atoms in the condensate, ![]() is the reduced mass, and
is the reduced mass, and ![]() is the density of the BEC.
is the density of the BEC.
Of importance to us is the interaction Hamiltonian between the trapping well potential and the BEC serving as a thermal bath for excitations. We derive this Hamiltonian as follows: first we make use of the field operators corresponding to the system ![]() and the bath
and the bath ![]() . Explicitly, those field operators have the following form:
. Explicitly, those field operators have the following form:
(4) ![Rendered by QuickLaTeX.com \begin{align*} \hat{\psi}_{s}&=\left[\varphi_{g,1}(x)a_{g,1}+\varphi_{g,2}(x)a_{g,2}+\varphi_{e_{1},0}(x)a_{e_{1},0}+\varphi_{e_{2},0}(x)a_{e_{2},0}\right]w(y)w(z),\nonumber\\ \hat{\psi}_{b}&=\sqrt{\rho_b}+\delta\hat{\psi}_{b}(\mathbf{r}),\;\;\;\delta\hat{\psi}_{b}(\mathbf{r})=\frac{1}{\sqrt{V}}\sum_\mathbf{k}\left(u_{\mathbf{k}}b_\mathbf{k}e^{i\mathbf{k}\cdot\mathbf{r}}+v_{\mathbf{k}}b^{\dagger}_\mathbf{k}e^{-i\mathbf{k}\cdot\mathbf{r}}\right). \end{align*}](https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-0d0b69f6f15acb6906fc9b9bbe2eb0bb_l3.png)
Here, ![]() and
and ![]() are wavefunctions in the transverse directions of the trapping potential,
are wavefunctions in the transverse directions of the trapping potential, ![]() and
and ![]() ,
, ![]() ,
, ![]() is the condensate energy,
is the condensate energy, ![]() is the condensate velocity and
is the condensate velocity and ![]() is the interaction strength between the condensate’s atoms. The interaction Hamiltonian will then have the form
is the interaction strength between the condensate’s atoms. The interaction Hamiltonian will then have the form
(5) ![]()
with only the terms linear in ![]() and
and ![]() evaluated. Evaluating this integral gives us the expression for
evaluated. Evaluating this integral gives us the expression for ![]() given in Eq. (2).
given in Eq. (2).
In the interaction Hamiltonian, we find that integrals of the following form will appear:
(6) 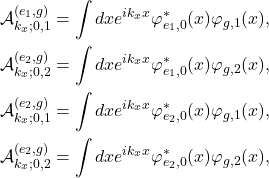
where ![]() ,
, ![]() are the ground and first excited state eigenfunctions for a harmonic oscillator. The wavefunctions
are the ground and first excited state eigenfunctions for a harmonic oscillator. The wavefunctions ![]() and
and ![]() are, by definition, even and odd functions, respectively, i. e.
are, by definition, even and odd functions, respectively, i. e. ![]() and
and ![]() . Furthermore, due to the symmetry of the system, we note that for the ground state eigenfunctions,
. Furthermore, due to the symmetry of the system, we note that for the ground state eigenfunctions, ![]() . Hence, by making use of these relations and by changing the variable of integration from
. Hence, by making use of these relations and by changing the variable of integration from ![]() to
to ![]() in Eq. (6), we then obtain the following relations:
in Eq. (6), we then obtain the following relations:
(7) 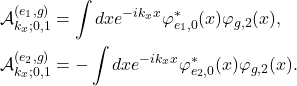
This then implies the following relations between the overlap integrals:
(8) ![]()
We note that from the configuration of the trapping potential, ![]() , where
, where ![]() and
and ![]() are the widths of the wavefunctions corresponding to the wells and the harmonic potential, respectively. Thus,
are the widths of the wavefunctions corresponding to the wells and the harmonic potential, respectively. Thus,
(9) ![]()
wherein we assume that the ground state wavefunction ![]() is a Gaussian wavefunction with width
is a Gaussian wavefunction with width ![]() ,
,
(10) 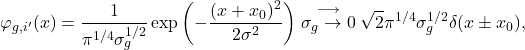
and the plus and minus signs correspond to ![]() and
and ![]() , respectively. We can then substitute these terms back into the interaction Hamiltonian, and we find that
, respectively. We can then substitute these terms back into the interaction Hamiltonian, and we find that ![]() is a function of the operators
is a function of the operators ![]() , where
, where ![]() and
and ![]() , and
, and ![]() and
and ![]() .
.
Having derived the interaction Hamiltonian for our system, we then proceed, in the next explainer post of this series, to derive the master equation describing the dynamics of this system corresponding to our dissipative quantum state preparation scheme.
Reference:
R. C. F. Caballar, S. Diehl, H. Makela, M. Oberthaler and G. Watanabe, Phys. Rev. A 89, 013620 (2014)
Further reading:
S. Diehl, A. Micheli, A. Kantian, B. Kraus, H. P. Buchler, and P. Zoller, Nat. Phys. 4, 878 (2008)
F. Verstraete, M. M. Wolf and J. I Cirac, Nat. Phys. 5, 633 (2009)
F. Pastawski, L. Clemente and J. I. Cirac, Phys. Rev. A 83,1 (2011)
E. G. Dalla Torre, J. Otterbach, E. Demler, V. Vuletic and M. D. Lukin, Phys. Rev. Lett 110, 120402 (2013)