Who is afraid of divergent integrals?

By | July 29, 2015
2 Comments

We, physicists, are obviously not afraid. Our literature, from our notes to our papers to our books, is replete with them. We are not at all embarrassed by our seemingly wanton disregard to mathematical rigor in our mathematical acrobatics that often lead to our ill-defined or infinite-valued divergent integrals. Our enduring affair with such almost chimerical mathematical objects is a testament to the fact that our “lack of respect” to analytical accuracy is often rewarded with a deeper insight into nature and, to some, by the Nobel Prize. Think of quantum electrodynamics: It is our most accurate theory so far and yet laden with divergent integrals.

By some sort of sorcery, we summon meaningful values out of our dubious integrals. Not only that we can extract a value but we can seemingly extract at will any value from them to suit our liking; in particular, a divergent integral can be assigned multiple values at once. It is as if divergence is a bottomless well from which we can draw any amount of water at our disposal. The fact that we can associate different values to a single divergent expression is disquieting. For if no unique value can be associated to a divergent integral, then what meaning can be attached to the integral itself?

In this post, I discuss how a divergent integral may arise naturally as a solution to a well-defined physical problem, and demonstrate how a single divergent integral can take on different meaningful finite values, and how such non-uniqueness of assignable value to the integral may warrant the interpretation that a divergent integral can be meaningfully interpreted as a representation of a whole class of solution to a given problem.

The divergent integral appears in quantum field theory and assumes an arbitrary value there.

The divergent integral appears in quantum field theory and assumes an arbitrary value there.

Quantum scattering and its divergent integral

Our purpose is best demonstrated by quantum scattering theory, which takes the scattering amplitude as the object of computation. The derivation of the amplitude translates into solving the differential equation

(1)   \begin{equation*} (\nabla^2 + k^2) G({\bf r}) = - 4 \pi \delta({\bf r}), \end{equation*}

where G({\bf r}) is known as a Green’s function, \delta({\bf r}) is the Dirac delta function and k is the incident kinetic energy. The Green’s function is typically solved by assuming a solution in Fourier integral form

(2)   \begin{equation*} G({\bf r})= \int_{\mathbb{R}^3} g({\bf k}') e^{i {\bf k}'\cdot {\bf r}} \mbox{d}^3k', \end{equation*}

where g({\bf k}) is to be determined. Also, the Dirac delta function is written as the Fourier integral

(3)   \begin{equation*} \delta({\bf r})=\frac{1}{(2 \pi)^{3/2}} \int_{\mathbb{R}^3} \mbox{e}^{i {\bf k}\cdot {\bf r}} \mbox{d}k^3 \end{equation*}

Equations \eqref{solution} and \eqref{delta} are substituted back into the differential equation to obtain g({\bf k}). After some simplifications the solution assumes the form

(4)   \begin{equation*} G({\bf r})=-\frac{1}{\pi r} \frac{\mbox{d} }{\mbox{d}r} \int_{-\infty}^{\infty} \frac{\mbox{e}^{i k' r}}{k'^2 - k^2 } \, \mbox{d}k'. \end{equation*}

The integrand in equation \eqref{integral} has poles at k'=\pm k which lie along the range of integration so that the integral does not exist. This is an example of a divergent integral that arises naturally from a physical problem. But why have we ended up with a divergent integral for a solution? The source of the divergence can be traced from at least two formal manipulations—mathematical steps performed without regard to rigor—that we have made in arriving at equation \eqref{integral}.

First, we were already confused with the meaning of the integral in the assumed solution \eqref{solution} because the integral in the representation of the Dirac delta function in \eqref{delta} was not an integral in the same sense as we would like to interpret the integral in \eqref{solution}. The integral in \eqref{delta} is at most divergent if we insist in interpreting it as an integral. Second, we committed the haphazard interchange of the integration and the differentiation in substituting back the assumed integral solution to the differential equation which is generally not valid.

The divergence in our solution is the penalty we have paid for our formal manipulations.

The many values of a divergent integral

Should we then dismiss the divergent solution we have obtained? A pedant (not necessarily a mathematician) would out-rightly brand it worthless. But the physicist has an uncanny intuition over such ill-defined objects. Indeed, we can extract meaningful solution from the divergent solution, and by that we mean we can obtain from it physically meaningful solutions to the original physics problem.

We glean insight into how to accomplish the feat by noting that we arrived at the divergence from a haphazard interchange of generally non-commuting operations, integration and differentiation in our case. (Two operations are said to commute if their order of applications does not matter.) Perhaps we can reverse the divergence by introducing two operations that do not commute and then by arbitrarily interchanging the operations, and hope to obtain a finite value.

There are clearly many pairs of non-commuting operations that we can think of. Let us try

(5)   \begin{eqnarray*} \int_{-\infty}^{\infty} \frac{\mbox{e}^{i k' r}}{k'^2 - k^2 } \, \mbox{d}k' &=& \int_{-\infty}^{\infty} \lim_{\epsilon\rightarrow 0^+} \frac{\mbox{e}^{i k' r}}{k'^2 - (k^2 + i \epsilon)} \, \mbox{d}k'\\ &=&\lim_{\epsilon\rightarrow 0^+}\int_{-\infty}^{\infty} \frac{\mbox{e}^{i k' r}}{k'^2 - (k^2 + i \epsilon)} \, \mbox{d}k' \end{eqnarray*}

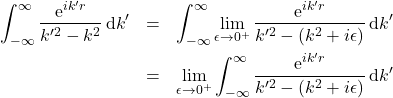
where we have freely interchanged the order of integration and the limiting operation in the second line. Integration and taking limits do not commute, but we went ahead with the interchange anyway, and valiantly maintained the equality sign. Notice now that we are left with an absolutely convergent integral for \epsilon>0. Evaluating the integral and followed by taking the limit yield

(6)   \begin{equation*} \int_{-\infty}^{\infty} \frac{\mbox{e}^{i k' r}}{k'^2-k^2}\, \mbox{d}k' = i \pi \frac{\mbox{e}^{i k r}}{k}. \end{equation*}

And we are led to a well-defined function of r that we can assign as a value of the divergent integral.

But that is not the only value that we can obtain from the divergent integral. We perform a similar set of operations only that the sign of \epsilon is now reversed,

(7)   \begin{eqnarray*} \int_{-\infty}^{\infty} \frac{\mbox{e}^{i k' r}}{k'^2 - k^2 } k' \, \mbox{d}k' &=& \int_{-\infty}^{\infty} \lim_{\epsilon\rightarrow 0^+} \frac{\mbox{e}^{i k' r}}{k'^2 - (k^2 - i \epsilon)} \, \mbox{d}k'\\ &=&\lim_{\epsilon\rightarrow 0^+}\int_{-\infty}^{\infty} \frac{\mbox{e}^{i k' r}}{k'^2 - (k^2 - i \epsilon)} \, \mbox{d}k' . \end{eqnarray*}

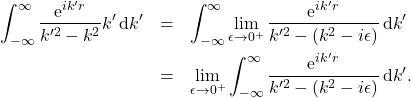
Again the integral in the second line is absolutely convergent and the limit exists. It, however, now assigns a different value,

(8)   \begin{equation*} \int_{-\infty}^{\infty} \frac{\mbox{e}^{i k' r}}{k'^2-k^2}\, \mbox{d}k' = - i \pi \frac{\mbox{e}^{- i k r}}{k}, \end{equation*}

to the integral.

Yet another value can be extracted by using a different limiting scheme. For \epsilon>0, we introduce the limit

(9)   \begin{eqnarray*} \int_{-\infty}^{\infty} \frac{\mbox{e}^{i k' r}}{k'^2 - k^2 } k' \, \mbox{d}k' &=& \lim_{\epsilon\rightarrow 0}\left[\int_{-\infty}^{-(k-\epsilon)} \frac{\mbox{e}^{i k' r}}{k'^2 - k^2 } k' \, \mbox{d}k' \right. \nonumber \\ &&\hspace{12mm} + \int_{-(k+\epsilon)}^{(k-\epsilon)} \frac{\mbox{e}^{i k' r}}{k'^2 - k^2 } k' \, \mbox{d}k'\nonumber \\ && \left. \hspace{12mm}+ \int_{(k+\epsilon)}^{\infty} \frac{\mbox{e}^{i k' r}}{k'^2 - k^2 } k' \, \mbox{d}k'\right]. \end{eqnarray*}

We maintain the formal equality if we perform the limit followed by integration. But we reverse the order to perform the integration first followed by the limit. This gives a well-defined value which is just the well-known Cauchy principal value of the integral. The result is

(10)   \begin{eqnarray*} \int_{-\infty}^{\infty} \frac{\mbox{e}^{i k' r}}{k'^2 - k^2 } \, \mbox{d}k'= - \pi \frac{\sin\, kr}{k}, \end{eqnarray*}

which happens to be he average of the above two earlier values.

The many values are not bad at all

What is happening? We seem to extract any value at will from the divergent integral. It is clear at this point that giving a finite value to a non-existent integral is not at all a problem. What is troubling is the lack of uniqueness that can be ascribed to the integral. This non-uniqueness leads us to the following three distinct Green function solutions

(11)   \begin{equation*} G_{\pm}(\mathbf{r})=\frac{\mbox{e}^{\pm i k r}}{r}, \;\;\; G_0(\mathbf{r})=\frac{\cos \, kr}{r} , \end{equation*}

obtained by substituting equations \eqref{pek1}, \eqref{pek2} and \eqref{pek3} back into equation \eqref{integral}. That these are indeed solutions can be verified by showing that they satisfy the differential equation \eqref{de}. Since they depend on the radial coordinate r alone, it is sufficient to verify that they satisfy

(12)   \begin{equation*} \left(\frac{1}{r^2}\frac{\mbox{d}}{\mbox{d}r} r^2 \frac{\mbox{d}}{\mbox{d}r} + k^2\right)G_{\sigma}(\mathbf{r})=- \frac{\delta(r)}{r^2}, \end{equation*}

for \sigma=\pm, 0.

What meaning can we attach to these different Green functions? It turns out that they are solutions satisfying specific boundary conditions at infinity. The solution G_+ corresponds to a scattered, expanding spherical wave away from the scattering center. On the other hand, the solution G_- corresponds to a collapsing spherical wave coming from infinity towards the scatterer. The solution G_0 corresponds to the simultaneous presence of expanding and collapsing spherical wave at infinity. Clearly, the different extracted values of the divergent integral are meaningful as they correspond to solutions satisfying certain boundary conditions.

This observation suggests that a divergent integral can be taken to represent the general solution of a given differential equation, with the different ways of interpreting the integral as implementing specific boundary conditions. Viewed as a general solution, we can appreciate that it has to be divergent or lacking a definite value otherwise it cannot be a general solution in the first place. What comes to mind is the general solution of, say, a second order differential equation, which is given by y(x)=a_1 f_1(x) + a_2 f_2(x), were a_1 and a_2 are arbitrary constants, and f_1(x) and f_2(x) are two linearly independent solutions of the differential equation. The general solution y(x) does not possess a definite value, but different specific solutions can be obtained from f(x) by imposing initial or boundary conditions. Only after conditions have been imposed that specific solutions and definite values are obtained.

Conclusion

Entertaining divergent integrals has not been a problem for the physicist. There is no shortage of possible means of committing a divergent integral to a specific value. We have the famous principal value, the distributional value by the theory of distributions, the analytic value by analytic continuation, the Hadamard value, the not so familiar Reiz regularized value, to name some of the widely used way of assigning value to divergent integrals. Thanks to our friends from the Mathematics Department. So there is really not much to be scared about with our ill-defined and non-existent integrals—we can always somehow find a way to endow meaning to them.

But what can be disturbing is the fact that the above-enumerated means of giving value to the integral do not necessarily agree. So which is correct? The insight provided by quantum scattering theory raises the possibility of interpreting a given divergent integral as some kind of a general solution with the different assignable values as implementations of specific sets of conditions. So we ask, Given a divergent integral, can we find, say, a differential equation that takes the divergent integral as its formal general solution with the different values that can be extracted from it as specific solutions satisfying initial or boundary conditions?

2 thoughts on “Who is afraid of divergent integrals?”

Leave a Reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.