Introduction
The dynamics of a quantum system plays out in a Hilbert space ![]() , which we, for simplicity’s sake, take here to be finite dimensional. In general the state of a closed quantum system, i.e. a system that does not exchange energy and information with another quantum system, is given by a vector
, which we, for simplicity’s sake, take here to be finite dimensional. In general the state of a closed quantum system, i.e. a system that does not exchange energy and information with another quantum system, is given by a vector ![]() in
in ![]() . Such a state is referred to as a pure state. The evolution of a pure state is dictated by the well-known Schrodinger equation
. Such a state is referred to as a pure state. The evolution of a pure state is dictated by the well-known Schrodinger equation
(1) ![]()
where ![]() is the system Hamiltonian. The Schrodinger equation can be rewritten in operator form using the density matrix representation,
is the system Hamiltonian. The Schrodinger equation can be rewritten in operator form using the density matrix representation,
(2) ![]()
where ![]() is the commutator and
is the commutator and ![]() is the density matrix corresponding to the pure state
is the density matrix corresponding to the pure state ![]() . Equation \eqref{vonneumann} is known as the von Neumann equation.
. Equation \eqref{vonneumann} is known as the von Neumann equation.
When the state of the system is pure, the Schrodinger and von Neumann equations are equivalent, and either equation can solve the dynamics of the system. However, when the system is in a mixed state, no vector or wave-function, ![]() , is associated with the state so that the Schrodinger equation \eqref{schrodinger} is not anymore the appropriate quantum equation of motion. For mixed states, the von Neumann equation \eqref{vonneumann} is the relevant dynamical equation to use. The equivalence of the Schrodinger and von Neumann equations is broken when the system is in a mixed state. This happens when the system is in a statistical ensemble of pure states, or when it is interaction with another system, in particular, immersed in some environment.
, is associated with the state so that the Schrodinger equation \eqref{schrodinger} is not anymore the appropriate quantum equation of motion. For mixed states, the von Neumann equation \eqref{vonneumann} is the relevant dynamical equation to use. The equivalence of the Schrodinger and von Neumann equations is broken when the system is in a mixed state. This happens when the system is in a statistical ensemble of pure states, or when it is interaction with another system, in particular, immersed in some environment.
In the later the interaction allows the exchange of information from one system to the other which leaves the system of interest in a mixed state. The evolution in the presence of a quantum environment, i.e., the evolution of an open quantum system, may take on different forms depending on the model of the interaction. For example, under certain approximations, the evolution assumes the well-known Lindblad Master equation,
(3) ![]()
where the ![]() ‘s are some operators in the system Hilbert space and the
‘s are some operators in the system Hilbert space and the ![]() ‘s are some real-valued functions of
‘s are some real-valued functions of ![]() . Equation \eqref{lindblad} generally evolves any initial state, including a pure state, into a mixed state.
. Equation \eqref{lindblad} generally evolves any initial state, including a pure state, into a mixed state.
Clearly, the dynamics of an open quantum system must be solved in terms of the density matrix and not through the wave-function. The most general evolution of the density matrix can be written as
(4) ![]()
where ![]() is an operation taking operators of the system Hilbert space into operators of the same Hilbert space. The von Neumann and Lindblad Master equations can be written in this form with the appropriate identifications of
is an operation taking operators of the system Hilbert space into operators of the same Hilbert space. The von Neumann and Lindblad Master equations can be written in this form with the appropriate identifications of ![]() .
.
The operation ![]() mapping density matrices into operators of
mapping density matrices into operators of ![]() is an example of a super-operator. It is referred to as a super-operator because it acts on operators of a Hilbert space
is an example of a super-operator. It is referred to as a super-operator because it acts on operators of a Hilbert space ![]() , not on the vectors of
, not on the vectors of ![]() . In this post, I give a quick introduction to super-operators and their underlying Hilbert space, and demonstrate how the von Neumann equation may be solved using the spectral resolution of the relevant super-operator in the quantum equation of motion of the density matrix.
. In this post, I give a quick introduction to super-operators and their underlying Hilbert space, and demonstrate how the von Neumann equation may be solved using the spectral resolution of the relevant super-operator in the quantum equation of motion of the density matrix.
Super-operators
Let us consider the finite dimensional complex Hilbert space ![]() for some integer
for some integer ![]() . Typical elements of
. Typical elements of ![]() are represented by column vectors with complex entries; that is, every element
are represented by column vectors with complex entries; that is, every element ![]() of
of ![]() is given by
is given by ![]() , where each
, where each ![]() is a complex number and
is a complex number and ![]() is the transpose operation. For every pair of elements
is the transpose operation. For every pair of elements ![]() and
and ![]() , the inner product is given by
, the inner product is given by ![]() . The whole Hilbert space structure of
. The whole Hilbert space structure of ![]() is dictated by this given inner product. (A brief introduction to Hilbert spaces is given here.)
is dictated by this given inner product. (A brief introduction to Hilbert spaces is given here.)
Operators in ![]() are operations that transforms each vector
are operations that transforms each vector ![]() of
of ![]() into another vector
into another vector ![]() of
of ![]() . In this post we are only interested with the linear operators. An operator
. In this post we are only interested with the linear operators. An operator ![]() in
in ![]() is linear if
is linear if ![]() , for every complex
, for every complex ![]() ,
, ![]() and vectors
and vectors ![]() ,
, ![]() . Any such linear operator is represented by
. Any such linear operator is represented by ![]() complex matrix in some chosen basis. We denote the set of all
complex matrix in some chosen basis. We denote the set of all ![]() complex matrices or the set of all linear operators in
complex matrices or the set of all linear operators in ![]() by
by ![]() . The set
. The set ![]() is a complex vector space under the usual rules of matrix addition and multiplication of matrices by complex numbers. From here on when ever we refer to
is a complex vector space under the usual rules of matrix addition and multiplication of matrices by complex numbers. From here on when ever we refer to ![]() as a vector space we mean it under the just stated rules of addition and multiplication.
as a vector space we mean it under the just stated rules of addition and multiplication.
Now a super-operator over the Hilbert space ![]() is a mapping of every operator in
is a mapping of every operator in ![]() into another operator in
into another operator in ![]() . That is if
. That is if ![]() is a super-operator over
is a super-operator over ![]() then for every operator
then for every operator ![]() in
in ![]() the mapping
the mapping ![]() is again an operator in
is again an operator in ![]() .
.
Example-1. Let ![]() be any operator in
be any operator in ![]() and let us define the super-operator
and let us define the super-operator ![]() by its action
by its action
(5) ![]()
for every operator ![]() in
in ![]() , where
, where ![]() is understood to be the matrix product of
is understood to be the matrix product of ![]() and
and ![]() . Since the matrix product of two
. Since the matrix product of two ![]() matrices is also an
matrices is also an ![]() matrix,
matrix, ![]() maps all
maps all ![]() into another operator. This super-operator is known as the right multiplication super-operator.
into another operator. This super-operator is known as the right multiplication super-operator.![]()
Example-2. Let ![]() be some operator in
be some operator in ![]() and define the superoperator
and define the superoperator ![]() by
by
(6) ![]()
for every operator ![]() in
in ![]() , where
, where ![]() is understood as the matrix product of
is understood as the matrix product of ![]() and
and ![]() . This is known as the left multiplication super-operator.
. This is known as the left multiplication super-operator.![]()
Example-3. Let ![]() be any operator in
be any operator in ![]() . Define the super-operator
. Define the super-operator ![]() by
by
(7) ![]()
where matrix multiplication is implied. This is just the super-operator representation of the well-known commutator of two operators.![]()
Example-4. Let ![]() be any operator again in
be any operator again in ![]() . Define the super-operator
. Define the super-operator ![]() by
by
(8) ![]()
This is the well-known anti-commutator of the operators ![]() and
and ![]() .
. ![]()
The Lindblad equation in super-operator form
By inspection of the Lindblad Master equation \eqref{lindblad}, we find that it can be written in terms of the above super-operators
(9) ![Rendered by QuickLaTeX.com \begin{equation*} \frac{\mbox{d}\rho}{\mbox{d}t}=\left[\frac{1}{i\hbar} \mathcal{L}_{H(t)}^{-} + \sum_k \gamma_k\left(\mathbf{L}_{L_k} \mathbf{R}_{L_k^{\dagger}} -\frac{1}{2} \mathcal{L}_{L_k^{\dagger}L_k}^{+}\right)\right]\rho(t) \end{equation*}](https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-ebb16d3d212ceb0eb09fbeee43a6e12f_l3.png)
from which we identify the super-operator ![]() in equation \eqref{general} to be given by
in equation \eqref{general} to be given by
(10) ![Rendered by QuickLaTeX.com \begin{equation*} \mathcal{L}_t=\left[\frac{1}{i\hbar} \mathcal{L}_{H(t)}^{-} + \sum_k \gamma_k(t)\left(\mathbf{L}_{L_k} \mathbf{R}_{L_k^{\dagger}} -\frac{1}{2} \mathcal{L}_{L_k^{\dagger}L_k}^{+}\right)\right]. \end{equation*}](https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-5f7a78b596974ae2664a2e92406fb613_l3.png)
Super-Hilbert Spaces
In solving problems involving super-operators, such as in solving the von Neumann equation, spectral decomposition of the super-operator involved is usually needed. This will require questions of hermicity or normality of the super-operators involved. But this is only possible if we endow the vector space of operators ![]() with a Hilbert space structure. This requires defining an inner product for every pair of operators in
with a Hilbert space structure. This requires defining an inner product for every pair of operators in ![]() , from which the norm and the metric of
, from which the norm and the metric of ![]() follow. For every pair of operators
follow. For every pair of operators ![]() and
and ![]() in
in ![]() , we define the complex valued functional
, we define the complex valued functional
(11) ![]()
where ![]() is the trace of a matrix and
is the trace of a matrix and ![]() is the adjoint of
is the adjoint of ![]() . In the following we will show that equation \eqref{bobo} is an inner product in
. In the following we will show that equation \eqref{bobo} is an inner product in ![]() .
.
Recall that an inner product on a vector space ![]() is a complex valued function
is a complex valued function ![]() over all pairs of vectors
over all pairs of vectors ![]() and
and ![]() in
in ![]() with the following properties: For every
with the following properties: For every ![]() and
and ![]() in
in ![]() , and scalars
, and scalars ![]() ,
, ![]() ,
,
-
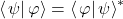 ,
, -
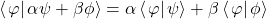 ,
, -
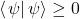 with equality only for
with equality only for 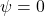 .
.
The pair ![]() is called an inner product space. Whenever the inner product is defined from the outset, we can refer to
is called an inner product space. Whenever the inner product is defined from the outset, we can refer to ![]() simply as an inner product space.
simply as an inner product space.
To show that equation \eqref{bobo} satisfies all the above axioms of an inner product we will need the following properties of the trace of a matrix,
-
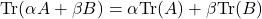 ,
, -
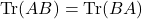 ,
, -
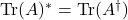 .
.
Also we will need the following properties of the adjoint of a matrix,
-
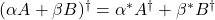
-
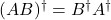
-
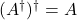
- V.E. Tarasov, Quantum mechanics of non-Hamiltonian and dissipative systems, Elsevier (2008).
It can now be readily established that the equation \eqref{inner} is indeed an inner product. For the first property,
(12) 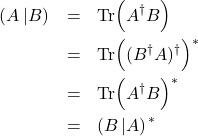
For the second property,
(13) 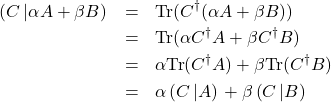
It is less straightforward to show the third property. Now ![]() . The operator
. The operator ![]() is hermitian and all its eigenvalues,
is hermitian and all its eigenvalues, ![]() ‘s, are zero or positive. Since the trace is the sum of the eigenvalues for hermitian matrices we have
‘s, are zero or positive. Since the trace is the sum of the eigenvalues for hermitian matrices we have ![]() , which is positive or zero. The sum of the eigenvalues vanishes only when all the eigenvalues are zero or
, which is positive or zero. The sum of the eigenvalues vanishes only when all the eigenvalues are zero or ![]() is itself the zero matrix. Then we have established
is itself the zero matrix. Then we have established
(14) ![]()
with an equality to zero provided ![]() . Thus we have established that equation \eqref{inner} is an inner product.
. Thus we have established that equation \eqref{inner} is an inner product.
The set of operators ![]() is now turned into a pre-Hilbert space by assigning its norm,
is now turned into a pre-Hilbert space by assigning its norm, ![]() , and metric,
, and metric, ![]() , in terms of the given inner product, specifically
, in terms of the given inner product, specifically
(15) ![]()
(16) ![]()
It can be established that the set ![]() is complete with respect to the metric induced by the inner product \eqref{inner}. Hence
is complete with respect to the metric induced by the inner product \eqref{inner}. Hence ![]() , together with the inner product
, together with the inner product ![]() , is a Hilbert space, which we call a super-Hilbert space. The name super-Hilbert space is appropriate to indicate that it is built upon another Hilbert space and the fact that it is the domain of super-operators. From here on, whenever we refer to
, is a Hilbert space, which we call a super-Hilbert space. The name super-Hilbert space is appropriate to indicate that it is built upon another Hilbert space and the fact that it is the domain of super-operators. From here on, whenever we refer to ![]() as a super-Hilbert space we mean
as a super-Hilbert space we mean ![]() together with its inner product
together with its inner product ![]() .
.
An orthonormal basis of ![]() is a set of operators in
is a set of operators in ![]() ,
, ![]() , with the property
, with the property ![]() . Every operator
. Every operator ![]() in
in ![]() admits a Fourier expansion in terms of this basis,
admits a Fourier expansion in terms of this basis,
(17) 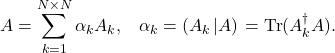
A set consisting of ![]() number of linearly independent operators that are not pairwise orthogonal can be turned into an orthonormal basis by means of the Gram–Schmidt orthogonalization process.
number of linearly independent operators that are not pairwise orthogonal can be turned into an orthonormal basis by means of the Gram–Schmidt orthogonalization process.
Example: The super-Hilbert space ![Rendered by QuickLaTeX.com M[\mathbb{C}^2]](https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-9d9e78a6d2203ba69fe40eac1ab1b800_l3.png)
It is well-known that any ![]() complex matrix can be uniquely represented in the following form,
complex matrix can be uniquely represented in the following form,
(18) ![]()
where ![]() is the
is the ![]() identity matrix and the
identity matrix and the ![]() ‘s are the spin Pauli matrices, and the coefficients
‘s are the spin Pauli matrices, and the coefficients ![]() ‘s are given by
‘s are given by
(19) ![]()
In standard representation, the spin Pauli matrices assume the form
(20) ![]()
(21) ![]()
(22) ![]()
By inspection of the expansion \eqref{tbt} and the coefficients \eqref{coeffs}, we recognize that the scheme of expanding any ![]() matrix in terms of the identity and the spin Pauli matrices can be naturally accommodated in super-Hilbert space formalism. In particular, we find that the coefficients \eqref{coeffs} can be expressed as the inner product of
matrix in terms of the identity and the spin Pauli matrices can be naturally accommodated in super-Hilbert space formalism. In particular, we find that the coefficients \eqref{coeffs} can be expressed as the inner product of ![]() with the identity and Pauli matrices. This leads us to the 4-dimensional super-Hilbert space
with the identity and Pauli matrices. This leads us to the 4-dimensional super-Hilbert space ![]() , which is spanned by the following set of hermitian operators
, which is spanned by the following set of hermitian operators
(23) ![]()
This set is an orthonormal set with respect to the inner product \eqref{bobo}, i.e. ![]() .
.
The adjoint of super-operators
Given the inner product we can now inquire whether a given super-operator is hermitian or not. Let ![]() be an everywhere defined operator in a Hilbert space
be an everywhere defined operator in a Hilbert space ![]() . The adjoint of
. The adjoint of ![]() is the unique operator, denoted by
is the unique operator, denoted by ![]() , such that
, such that ![]() , for all vectors
, for all vectors ![]() and
and ![]() in
in ![]() . This definition of the adjoint extends to the super-Hilbert space
. This definition of the adjoint extends to the super-Hilbert space ![]() , being a Hilbert space itself. So given a super-operator
, being a Hilbert space itself. So given a super-operator ![]() , its adjoint,
, its adjoint, ![]() , is the super-operator that satisfies the equality
, is the super-operator that satisfies the equality ![]() for all operators
for all operators ![]() and
and ![]() in
in ![]() . The super-operator
. The super-operator ![]() is hermitian if
is hermitian if ![]() . And if it is hermitian, it posseses a complete set of orthonormal eigen-operators with corresponding real eigenvalues.
. And if it is hermitian, it posseses a complete set of orthonormal eigen-operators with corresponding real eigenvalues.
Example-1. Let us obtain the adjoint of the right multiplication super-operator ![]() . For every pairs of operator
. For every pairs of operator ![]() and
and ![]() in
in ![]() we have
we have
(24) 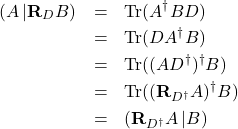
From the definition of the adjoint, we can now identify the desired adjoint
(25) ![]()
Clearly ![]() is hermitian provided
is hermitian provided ![]() is hermitian itself.
is hermitian itself.
Example-2. Following the same steps, we can establish that the left multiplication super-operator has the adjoint
(26) ![]()
Similarly ![]() is hermitian if
is hermitian if ![]() is itself hermitian.
is itself hermitian.
Example-3. Let us obtain the adjoint of the super-operator ![]() . For every pair of operators
. For every pair of operators ![]() and
and ![]() we have
we have
(27) 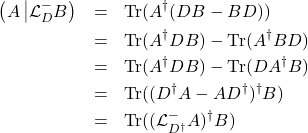
We can now identify the desired adjoint
(28) ![]()
When ![]() is hermitian,
is hermitian, ![]() is hermitian.
is hermitian.
Example-4. The super-operator ![]() has the adjoint
has the adjoint
(29) ![]()
so that it is hermitian when ![]() is itself hermitian.
is itself hermitian.
Solving the von Neumann equation in super-operator form: An example
As a simple example of the application of super-operators in quantum dynamics, let us consider solving the von Neumann equation
(30) ![]()
in the super Hilbert space ![]() , where
, where ![]() is a constant, given the initial state
is a constant, given the initial state ![]() . The solution is given by
. The solution is given by
(31) ![]()
The usual way of implementing this solution is by expansion of the exponential, which requires term by term evaluation and explicit summation of the resulting infinite series.
But the solution can be obtained without expansion by means of the spectral resolution of the super-operator ![]() . Since
. Since ![]() is hermitian, as established above, and since the dimension of the super-Hilbert space is 4, it has a complete set of orthonormal eigen-operators,
is hermitian, as established above, and since the dimension of the super-Hilbert space is 4, it has a complete set of orthonormal eigen-operators, ![]() , with real corresponding eigenvalues,
, with real corresponding eigenvalues, ![]() , i.e.,
, i.e., ![]() ; the eigen-values need not be distinct. The initial state,
; the eigen-values need not be distinct. The initial state, ![]() , can then be expanded in terms of these eigen-operators,
, can then be expanded in terms of these eigen-operators, ![]() , which by substitution to the solution yields
, which by substitution to the solution yields
(32) 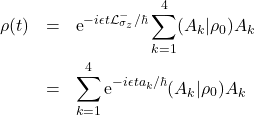
where we have used the linearity of ![]() and the equality
and the equality ![]() to obtain equation \eqref{ke}.
to obtain equation \eqref{ke}.
The problem now reduces to solving the eigenvalue problem for the super-operator ![]() . First let us consider those with zero eigenvalues, i.e., those that span the null space of
. First let us consider those with zero eigenvalues, i.e., those that span the null space of ![]() . These are just those that commute with
. These are just those that commute with ![]() . We readily obtain the identity operator
. We readily obtain the identity operator ![]() and
and ![]() itself, which are orthogonal and span the null space. We now solve the eigenvalue problem
itself, which are orthogonal and span the null space. We now solve the eigenvalue problem
(33) ![]()
where ![]() is a
is a ![]() matrix and
matrix and ![]() is a non-zero scalar. We expect to obtain two eigen-operators for we have already two coming from the null space.
is a non-zero scalar. We expect to obtain two eigen-operators for we have already two coming from the null space.
We expand ![]() in terms of the identity and the spin-Pauli matrices, which constitute an orthogonal basis in
in terms of the identity and the spin-Pauli matrices, which constitute an orthogonal basis in ![]() as discussed above,
as discussed above,
(34) ![]()
where the ![]() ‘s are scalars to be determined. We substitute the expansion \eqref{expand} back into the eigenvalue relation \eqref{eigen} and use the following known commutation relation to evaluate the action of the super-operator,
‘s are scalars to be determined. We substitute the expansion \eqref{expand} back into the eigenvalue relation \eqref{eigen} and use the following known commutation relation to evaluate the action of the super-operator,
(35) ![]()
Imposing the linear independence of the basis operators, we obtain the system of equations
(36) ![]()
(37) ![]()
Dividing the two expression in \eqref{exp} yields the eigenvalue equation ![]() , from which we obtain the two eigenvalues
, from which we obtain the two eigenvalues
(38) ![]()
Substituting these back into equations \eqref{exp} yields the normalized eigen-operators
(39) ![]()
One can check that ![]() and
and ![]() are orthogonal, i.e.,
are orthogonal, i.e., ![]() . Then we have the orthonormal eigen-operators
. Then we have the orthonormal eigen-operators ![]() with the corresponding eigenvalues
with the corresponding eigenvalues ![]() .
.
Substituting the eigen-operators and the eigenvalues back into equation \eqref{ke} finally yields the desired solution,
(40) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \rho(t)&=& \frac{1}{2} [\mathbb{I} + \rho_{0z}\sigma_z] \nonumber \\ && + \frac{1}{2} \left[\cos(2\epsilon t/\hbar) \rho_{0x} - \sin(2\epsilon t/\hbar)\rho_{0y}\right]\sigma_x\nonumber \\ && +\frac{1}{2} \left[\sin(2\epsilon t/\hbar) \rho_{0x} + \cos(2\epsilon t/\hbar)\rho_{0y}\right]\sigma_y \end{eqnarray*}](https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-5a0b4630c15253ea903e0aaa720592be_l3.png)
where ![]() with
with ![]() .
.
Further reading
For an in-depth discussion of super-operators, you may consult
I always was concerned in this subject and still am, thanks for putting up.
Thanks for dropping by.