Explainer Part 1: “Exactly decohering quantum measurement without environment” E.A. Galapon, arXiv:1505.06908, 26 May 2015.

The paper deals with the fundamental question of whether an environment is necessary or not to enforce quantum decoherence on quantum measuring instruments. The paper gives an unambiguous answer to the question as summarized by its Abstract:

Current quantum orthodoxy claims that the statistical collapse of the wave-function arises from the interaction of the measuring instrument with its environment through the phenomenon known as environment-induced decoherence. Here it is shown that there exists a measurement scheme that is exactly decohering without the aid of an environment. The scheme relies on the assumption that the meter is decomposable into probe and pointer, with the probe taken to be inaccessible for observation. Under the assumption that the probe and the pointer initial states are momentum limited, it is shown that coherences die out within a finite interval of time and the pointer states are exactly orthogonal. These lead to the fundamental realization that the dispersion of correlation does not require an external infinite number of degrees of freedom. An internal one degree of freedom is already sufficient to delocalize the correlations and leave its subparts in a classical mixed state so that decoherence may occur even for isolated measuring instruments.

This post is the first of a planned three-part series to give the necessary background of the paper.

Dynamics of Quantum Measurement

In a quantum measurement, a system is prepared in an initial state and allowed to interact with a measuring instrument until a reading is established. It is presumed that the measurement process is itself described by the rules of quantum mechanics. That is the whole process play out in a separable complex Hilbert space $\mathcal{H}$ , which includes the system subject to measurement and all relevant ancilla that come into play in the measurement process. The specific structure of $\mathcal{H}$ depends on the measurement model. The Schrödinger equation is then assumed to apply to the state space of $\mathcal{H}$ , which tacitly assumes that $\mathcal{H}$ describes a closed quantum system. This assumption of closedness can always be satisfied by the appropriate expansion of the whole system comprising the measurement process.

A quantum measurement is then a time-dependent problem described by some interaction Hamiltonian, $H(t)$ , in $\mathcal{H}$ . Pure states, $|\psi(t)\rangle$ , of $\mathcal{H}$ then evolve according to the Schrodinger equation

(1) $\begin{equation*} i\hbar \frac{\mbox{d}|\psi(t)\rangle}{\mbox{d}t} = H(t) |\psi(t)\rangle, \end{equation*}$

subject to some initial condition $|\psi(t_0)\rangle$ . The solution of which is given by

(2) $\begin{equation*} |\psi(t)\rangle = U(t,t_0) |\psi(t_0)\rangle \end{equation*}$

where $U(t,t_0)$ is the time evolution operator.

Various means of solving the time evolution operator exist, but the solution by means of the Magnus expansion is most relevant to the measurement models we are concerned here. The solution is given by

(3) $\begin{equation*} U(t,t_1)=\exp\left(\Omega(t,t_0)\right),\;\;\; \Omega(t,t_1)=\sum_{k=0}^{\infty} \Omega_k(,t_1) . \end{equation*}$

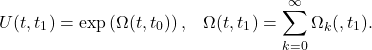
The first three terms of the expansion are given by

(4) $\begin{equation*} \Omega_1(t,t_1)=\frac{1}{i\hbar} \int_{t_0}^t \mbox{d}t_1\, H(t_1) , \end{equation*}$

(5) $\begin{equation*} \Omega_2(t,t_0)= \frac{1}{2 (i\hbar)^2} \int_{t_0}^t \mbox{d}t_1 \int_{t_1}^{t_0}\mbox{d}t_2\, [H(t_1),H(t_2)], \end{equation*}$

(6) $\begin{eqnarray*} \Omega_3(t,t_0)&=&\frac{1}{6 (i\hbar)^3}\int_{t_0}^t \mbox{d}t_1 \int_{t_0}^{t_1}\mbox{d}t_2 \int_{t_0}^{t_2} \mbox{d}t_3\nonumber\\ && \times \left([H(t_1),[H(t_2),H(t_3)]] + [H(t _3),[H(t_2),H(t_1)]]\right) . \end{eqnarray*}$

When the Hamiltonian, $H(t)$ , commutes at different times, i.e. $[H(t),H(t')]=0$ for all $t,t'$ , only the first term in the series contributes, so that the solution to the Schr\”{o}dinger equation is given by

(7) $\begin{equation*} |\psi(t)\rangle=\exp\left(-\frac{i}{\hbar}\int_{t_0}^{t}\mbox{d}\tau H(\tau)\right)|\psi(t_0)\rangle . \end{equation*}$

Quantum measurement is generally modeled by a time dependent Hamiltonian that commutes with itself for all times, in particular, of the form $H(t)= g(t) H_M$ , where $g(t)$ is a real valued function of time $t$ and $H_M$ is a time independent operator. It is assumed that $g(t)$ is non-vanishing only in the finite interval of time, $\Delta t = t_2-t_1$ , in which $t_1$ and $t_2$ are the times of start and end of the measurement, and that $\int_{t_1}^{t_2}g(t)\mbox{d}t=1$ . Then the state of the system right after the measurement interaction has ceased assumes the form

(8) $\begin{equation*} |\psi(t_2)\rangle=\mbox{e}^{-i H_M/\hbar} |\psi(t_1)\rangle . \end{equation*}$

In the paper, we referred to $H_M$ as the measurement Hamiltonian even though it does not have the unit of energy.

The von Neumann Measurement Scheme

Now let us consider a specific measurement model due to von Neumann. von Neumann’s model serves as the standard model upon which other models are patterned. Here we will consider the measurement of a non-degenerate observable $A$ of a finite dimensional quantum system $\mathcal{S}$ . We let $|\varphi_k\rangle$ be the eigenvectors of $A$ and $a_k$ the corresponding eigenvalues.

In the von Neumann scheme, the system $\mathcal{S}$ is coupled to a meter $\mathcal{M}$ . The system and the meter are both treated as quantum objects with respective Hilbert spaces $\mathcal{H}_S$ and $\mathcal{H}_M$ , with the system plus meter described by the tensor product Hilbert space $\mathcal{H}_S\otimes\mathcal{H}_M$ . It assumed that the free Hamiltonian of the systems involved is zero, or that the duration of measurement $\Delta t$ is much smaller than any relevant time scales of the free systems involved. The last one is true in particular when the measurement is impulsive.

Now the system and the meter are assumed to be initially prepared in the uncorrelated pure states, $|\psi_0\rangle$ and $|\phi_0\rangle$ , respectively, so that the composite initial state is given by $|\Psi\rangle=|\psi_0\rangle\!\!\otimes\!|\phi_0\rangle$ . The measurement is carried out by coupling the system observable $A$ with a meter observable $B$ , and is modeled by the measurement Hamiltonian

(9) $\begin{equation*} H_{M,\mbox{von}}=\lambda A\otimes B, \end{equation*}$

where $\lambda$ is a coupling constant (\cite{busch,von}). Then the state of the system and meter after the measurement interaction has ceased is given by

(10) $\begin{equation*} |\Psi_f\rangle=e^{ i \lambda A\otimes B/\hbar}|\psi_0\rangle\!\!\otimes\!|\phi_0\rangle. \end{equation*}$

Using the resolution of the identity provided by the eigenvectors of $A$ , the evolution operator becomes $e^{i \lambda A\otimes B/\hbar} = \sum_{k} |\varphi_k\rangle\!\!\!\langle\varphi_k| \otimes e^{i \lambda a_k B/\hbar}$ , from which we obtain the final state after the measurement

(11) $\begin{equation*} |\Psi_f\rangle=\sum_{k} \langle\varphi_k|\psi_0\rangle |\varphi_k\rangle \otimes |\phi_k\rangle, \end{equation*}$

where $|\phi_k\rangle=e^{i \lambda a_k B/\hbar} |\phi_0\rangle$ . The states, $|\phi_k\rangle$ ‘s, of the meter serve as pointer states. In order for the meter to provide an unambiguous reading the pointer states must necessarily be mutually orthogonal. That is they correspond to a hermitian (self-adjoint to be more precise) observable, $P$ , of the meter. We assume for now that the pointer states are mutually orthogonal. We defer a more thorough discussion of this issue in the next post.

The Basis Ambiguity Problem

Under the above assumption, the interaction has established a perfect correlation between the eigenstates of the system observable $A$ and the eigenstates of the meter observable $P$ with the correct probability amplitudes: the probability of finding the meter in the pointer state $|\phi_k\rangle$ is $|\langle\varphi_k|\psi_0\rangle|^2$ , which is the expected distribution of measurement on the observable $A$ . One may then think of equation \eqref{final} as a completed measurement. However, that is not the case because equation \eqref{final} can be written in a different basis leading to an ambiguity as to what was actually measured, a point elaborated by Zurek.

To appreciate the ambiguity problem, let us consider the object of measurement to be an observable of a qubit; moreover, let us assume that the meter is a qubit meter as well. Consider the system observable be the spin so that the state after the measurement is given by

(12) $\begin{equation*} |\psi_f\rangle = \frac{1}{\sqrt{2}} \left(|\uparrow\rangle\otimes|m_{\uparrow}\rangle + |\downarrow\rangle\otimes|m_{\downarrow}\rangle\right), \end{equation*}$

where $|\uparrow\rangle$ and $|\downarrow\rangle$ are the spin up and down states, respective; and $|m_{\uparrow}\rangle$ and $|m_{\downarrow}\rangle$ are the corresponding meter pointer states. The state \eqref{qubit} can be rewritten in terms of another set of basis vectors

(13) $\begin{equation*} |\nearrow\rangle=\frac{1}{\sqrt{2}} \left(|\uparrow\rangle + |\downarrow\rangle\right),\;\;\; |\swarrow\rangle=\frac{1}{\sqrt{2}} \left(|\uparrow\rangle - |\downarrow\rangle\right) \end{equation*}$

(14) $\begin{equation*} |m_{\nearrow}\rangle=\frac{1}{\sqrt{2}} \left(|m_{\uparrow}\rangle + |m_{\downarrow\rangle}\right),\;\;\; |m_{\swarrow}\rangle=\frac{1}{\sqrt{2}} \left(|m_{\uparrow}\rangle - |m_{\downarrow\rangle}\right) \end{equation*}$

These basis vectors correspond to different system and meter pointer observables. In these basis the final state \eqref{final} assumes the form

(15) $\begin{equation*} |\psi_f\rangle = \frac{1}{\sqrt{2}} \left(|\nearrow\rangle\otimes|m_{\nearrow}\rangle + |\swarrow\rangle\otimes|m_{\swarrow}\rangle\right). \end{equation*}$

In this form we see that the measurement interaction has not only established a perfect correlation between the states $\{|\uparrow\rangle,|\downarrow\rangle\}$ and $|m_{\uparrow}\rangle,|m_{\downarrow}\rangle$ but also the states $\{|\nearrow\rangle,|\swarrow\rangle\}$ and $|m_{\nearrow}\rangle,|m_{\swarrow}\rangle$ . In fact, the measurement interaction has established a correlation between an infinite number of pairs of system and meter observables. The question now naturally arises as to which exactly is measured. This is the basis ambiguity problem.

One may be tempted to interpret the ambiguity as a virtue that allows simultaneous measurement of different observables. However, since the two sets of states are non-orthogonal they correspond to two different sets of non-commuting observables. Then if we interpret the final wave-function as a completed measurement, then the two representations imply a simultaneous measurement of non-commuting observables, which cannot be the case. Equation \eqref{final} cannot then be considered as a completed measurement. It is for this reason that the state is referred to as a pre-measurement state.

von Neumann’s Statistical Collapse of the Wave-function

von Neumann recognized that equation \eqref{final} does not represent a completed measurement but needed to be supplemented to represent a completed measurement. This is implemented within the density matrix formalism of quantum mechanics.

In general, the state of a quantum system is represented by a density matrix, $\rho$ . A density matrix is an operator in the system Hilbert space with the following properties: its eigenvalues are either positive or zero, and the sum of its eigenvalues is equal to one. When $\rho$ is a projection operator, i.e. $\rho^2=\rho$ , $\rho$ is known to represent a pure state or a state represented by some Hilbert space vector $|\psi\rangle$ ; this is the state that every student of quantum mechanics is familiar with. When $\rho$ is not a projection operator, i.e. $\rho^2\neq \rho$ , it is known as a mixed state. When the system is in a pure state, there exists a measurement whose outcome is completely predictable. On the other hand, when the system is in a mixed state, no measurement on the system exists whose outcome can be predicted.

Quantum interference of mutually exclusive outcomes is manifested by the off-diagonal elements of the density matrix, known as the coherences. Pure states exhibit full coherence, and mixed states exhibit degraded coherence. Diagonal mixed states are states that do not exhibit any quantum interference at all. Since interference is the hallmark of a pure quantum system and the absence of interference is the hallmark of a classical system, a diagonal mixed state admit the interpretation as a classical state. This interpretation is reinforced by the fact that probabilities computed from such a density matrix satisfy the classical rules of probability. The density matrix then admits an ignorance interpretation.

Clearly the pre-measurement state \eqref{final} will not admit an ignorance interpretation because it is a pure state. Now the density matrix corresponding to the final state is $\rho_f=|\Psi_f\rangle\langle\Psi_f|$ and is explicitly given by

(16) $\begin{equation*} \rho_f = \sum_{k,l} \langle\varphi_k|\psi_0\rangle \langle\psi_0|\varphi_l\rangle |\varphi_k\rangle\langle\varphi_l| \otimes |\phi_k\rangle\langle\phi_l|. \end{equation*}$

The $k\neq l$ terms in this sum are the coherences and they arise from the linear superposition principle. In order for equation \eqref{che} to lead to a completed measurement of the observable $A$ , von Neumann postulated that, aside from the unitary evolution leading the system-meter initial state to the correlated state \eqref{che}, there is a non-unitary reduction of the state to an appropriate mixture,

(17) $\begin{equation*} \rho_f\mapsto \rho_f'=\sum_{k} |\langle\varphi_k|\psi_0\rangle|^2 |\varphi_k\rangle\langle\varphi_k| \otimes |\phi_k\rangle\langle\phi_l| . \end{equation*}$

The reduction is necessarily non-unitary because a unitary evolution maps a pure (mixed) state into a pure (mixed) state. After the reduction, the density matrix \eqref{cheche} is now diagonal and admits an ignorance interpretation for the measurement of the observable $A$ . This effectively solves the basis ambiguity problem.

The reduction of the density matrix from an initial pure state to a mixed state is referred to as the statistical collapse of the wave-function. It is natural to ask if this collapse of the wave-function can arise from the rules of quantum mechanics without postulation. It is the claim of quantum decoherence theory that von Neumann’s statistical collapse of the wave-function arises naturally from the Schrodinger equation. In Part II of the current explainer I will discuss quantum decoherence theory, in particular, the environment induced decoherence theory due to Zeh and Zurek.

Explainer Part 1: “Exactly decohering quantum measurement without environment” E.A. Galapon, arXiv:1505.06908, 26 May 2015.

Dynamics of Quantum Measurement

The von Neumann Measurement Scheme

The Basis Ambiguity Problem

von Neumann’s Statistical Collapse of the Wave-function

Further reading

Leave a Reply Cancel reply