Peres devoted a large part of Chapter 12 in the topic on the measurement of time in quantum mechanics. I quote Peres from Page 405, “The measurement of time is different from that quantities like position, momentum, energy, etc., because time is not a dynamical observable.” In Page 406 he continued, “What we call the measurement of time actually is the observation of some dynamical observable, the law of motion of which is known. For example, if we observe a free particle with classical Hamiltonian ![]() , the expression
, the expression ![]() satisfies
satisfies ![]() , and can, therefore, be considered as a `realization’ of time (for that particular Hamiltonian).”
, and can, therefore, be considered as a `realization’ of time (for that particular Hamiltonian).”
He then went on to quantize (through an exercise) the classical “realization of time” ![]() in momentum representation and obtained the eigenfunctions. He then concluded, “No simple physical meaning can be attributed to the results of the above exercise. If you want to try another exercise, take, instead of a free particle, a harmonic oscillator with
in momentum representation and obtained the eigenfunctions. He then concluded, “No simple physical meaning can be attributed to the results of the above exercise. If you want to try another exercise, take, instead of a free particle, a harmonic oscillator with ![]() . The result is even worse! In classical mechanics, you can define
. The result is even worse! In classical mechanics, you can define ![]() , which is multiple valued, just like the hour on an ordinary watch. But there is no such thing as a `multivalued operator’ in a correctly defined Hilbert space.”
, which is multiple valued, just like the hour on an ordinary watch. But there is no such thing as a `multivalued operator’ in a correctly defined Hilbert space.”
In this post I wish to bring to the reader’s attention that a meaningful quantization of such a multivalued classical observable can be made.
Let’s give an operational definition to the classical function ![]() in terms of the arrival time for us to have a firmer grasp of the underlying physics. Consider now an oscillator, whose Hamiltonian is given by
in terms of the arrival time for us to have a firmer grasp of the underlying physics. Consider now an oscillator, whose Hamiltonian is given by ![]() Let us interpret
Let us interpret ![]() and
and ![]() to be the initial position and momentum of the oscillator at time
to be the initial position and momentum of the oscillator at time ![]() . We now ask Given the initial position
. We now ask Given the initial position ![]() and momentum
and momentum ![]() at time
at time ![]() , what is the time
, what is the time ![]() that the oscillator will arrive at the origin? Solving the classical equations of motion and inverting them to solve for the time of arrival yield
that the oscillator will arrive at the origin? Solving the classical equations of motion and inverting them to solve for the time of arrival yield
(1) ![]()
which is just the negative of Peres’s time. That the time of arrival given by equation \eqref{ho} is multivalued is a consequence of the fact that the oscillator executes a periodic motion, so that there are infinitely many times the oscillator will arrive at or cross the origin.
Now while ![]() is multiple valued, the same cannot be said to the corresponding quantum observable, assuming it exists. The reason follows from the difference in the nature of measurements in classical and quantum mechanics. In classical mechanics, we can measure in principle without disturbing the system. This allows us to observe multiple arrivals and see the periodicity inherent in the classical expression. However, that cannot be said in the quantum case. In quantum mechanics, measurement irreversibly changes the state of the system. This means that the state of the system after the registration of the first arrival is no longer causally related to the initial state of the system or even just before the measurement was made. This means that if another arrival is registered after the first, the second cannot be interpreted as the second arrival starting from the initial state of the system.
is multiple valued, the same cannot be said to the corresponding quantum observable, assuming it exists. The reason follows from the difference in the nature of measurements in classical and quantum mechanics. In classical mechanics, we can measure in principle without disturbing the system. This allows us to observe multiple arrivals and see the periodicity inherent in the classical expression. However, that cannot be said in the quantum case. In quantum mechanics, measurement irreversibly changes the state of the system. This means that the state of the system after the registration of the first arrival is no longer causally related to the initial state of the system or even just before the measurement was made. This means that if another arrival is registered after the first, the second cannot be interpreted as the second arrival starting from the initial state of the system.
For this reason only the first arrival may only be meaningful to ask if we insist that arrival is interpreted as a detection at the arrival point. Under this understanding, Peres’s objection holds no ground. It may now be meaningful to ask if first time of arrival operators can be constructed. Technically the quantum observable corresponding to a classical observable is obtained by means of quantization. But quantization seems to present a problem for how can we quantize a classical expression that may be multivalued (or even complex)? The method of quantization of the classical time of arrival in the general case has been elucidated much earlier by myself here. In fact quantization there is only emergent, not something as a first principle or something to start with to obtain the corresponding quantum observable. But it is sufficient for me in this post to describe the quantization of equation \eqref{ho}.
The central idea in the quantization of the classical time of arrival is to restrict the classical time of arrival in a region of phase space containing the arrival point and where the arrival is unambiguously a first arrival. For the harmonic oscillator this is implemented by expanding the classical expression about the free time of arrival,
(2) 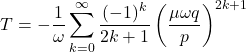
For ![]() equation \eqref{expanded} converges and it is the first time of arrival at the origin of the oscillator. It is equation \eqref{expanded} that we subject to quantization and not equation \eqref{ho}.
equation \eqref{expanded} converges and it is the first time of arrival at the origin of the oscillator. It is equation \eqref{expanded} that we subject to quantization and not equation \eqref{ho}.
We can then proceed with the quantization of the classical local time of arrival by means of the Weyl-Wigner quantization. Given a classical observable ![]() , it is quantized according to the prescription given by
, it is quantized according to the prescription given by
(3) ![]()
where the kernel is given by
(4) ![]()
The quantization is accomplished by interpreting the resulting integral as a distributional integral.
Weyl-Wigner quantization of equation \eqref{expanded} yield the following kernel for the quantized time of arrival operator
(5) 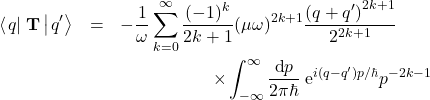
The integral, interpreted as a distributional integral, is evaluated using the known integral identity
(6) ![]()
Applying this to equation \eqref{kernel} yields
(7) 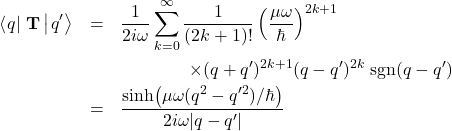
Observe that, while the classical function being quantized is meaningful only in a small region of the classical phase space, the resulting kernel of the quantized observable is defined everywhere in the ![]() -plane.
-plane.
Note that the classical observables ![]() and
and ![]() are canonically conjugate, i.e.
are canonically conjugate, i.e. ![]() , where
, where ![]() is the Poisson bracket. This conjugacy relation is carried over after quantization. It is readily verifiable that
is the Poisson bracket. This conjugacy relation is carried over after quantization. It is readily verifiable that ![]() and
and ![]() satisfy the canonical commutation relation
satisfy the canonical commutation relation ![]() . This relation is necessary for
. This relation is necessary for ![]() to have the necessary dynamical evolution with respect to the parametric time of the time-dependent Schrödinger equation.
to have the necessary dynamical evolution with respect to the parametric time of the time-dependent Schrödinger equation.
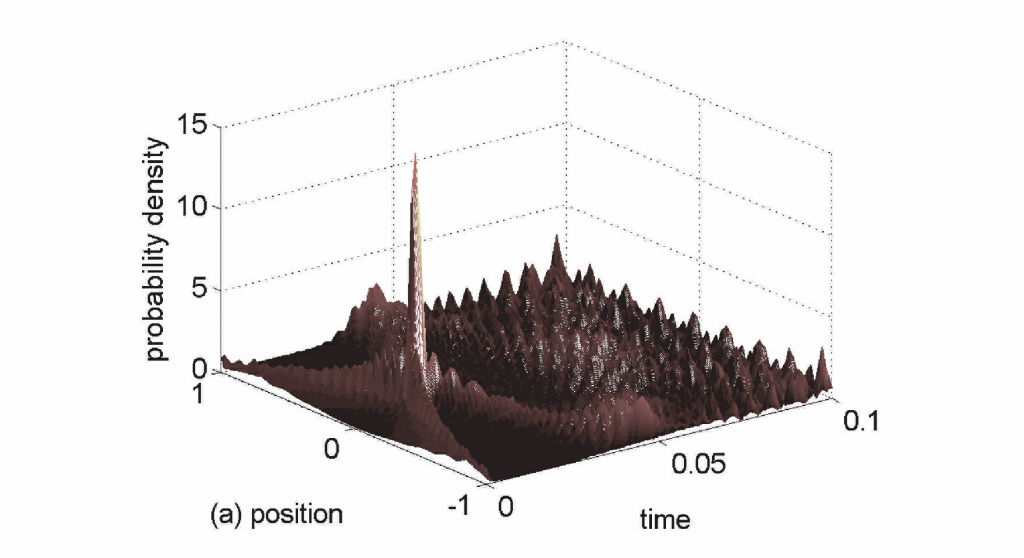
Figure-1. An eigenfunction of the harmonic oscillator time of arrival operator evolves such that it is most localized at the origin at the time equal to its corresponding eigenvalue. Source.
At this point, it is not clear how to interpret the quantized time of arrival operator. An insight into the physical meaning of the operator was obtained by means of coarse-graining the operator. We implemented the coarse-graining by confining the oscillator in an arbitrarily large box. And studied the properties of the operator in the confined configuration space. The eigenvalue problem of the coarse-grained operator was solved in particular. The eigenfunctions were then evolved using the time dependent Schrödinger equation. It was observed that the eigenfunctions evolve in such a way that the probability density became localized at the arrival point at their corresponding eigenvalues. We referred to this behavior as the unitary arrival of the eigenfunction at the arrival point. This is behavior is shown in Figure 1.
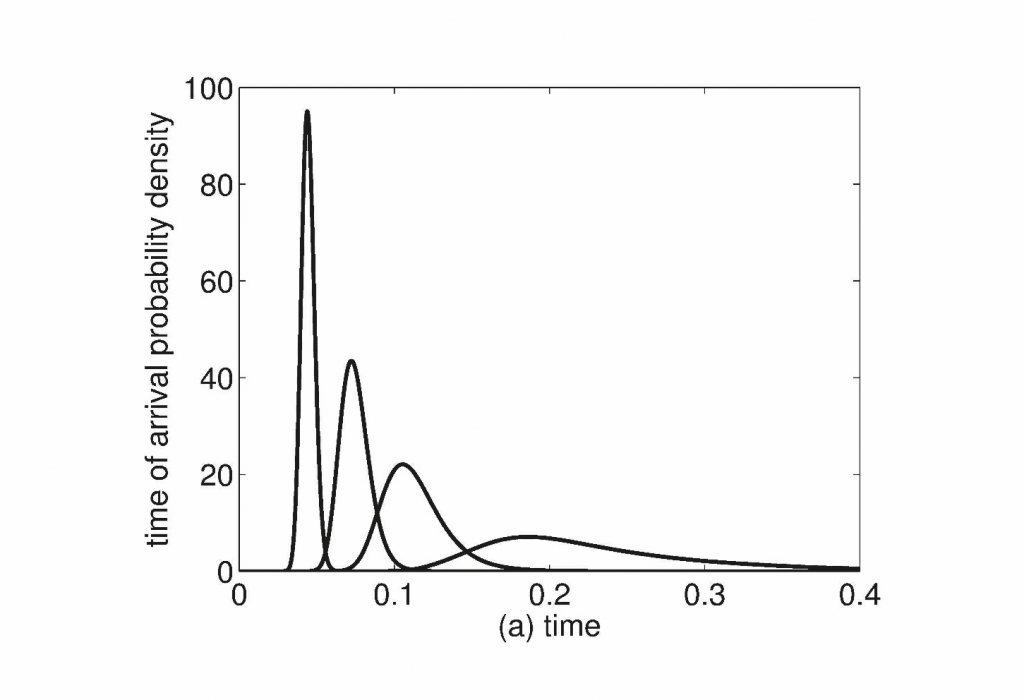
Figure-2. The time of arrival distribution for a Gaussian initial state for different incident kinetic energy. Source.
The coarse-graining allowed us also to compute time of arrival distributions that may be compared directly to results of time of arrival measurements on the oscillator. Figure 2 shows the time of arrival distributions for different initial Gaussian wave-functions. The short and fat distribution corresponds to low incident kinetic energy oscillator. The tall and localized distribution corresponds to a high incident kinetic energy. It is important to note that the distribution localizes to the value given by the classical expression in the high energy limit. This is the well-known quantum-classical correspondence principle at work. The principle says that the classical emerges from the quantum in the high energy regime, which is exactly what we observed from the computed arrival distributions.
The observed unitary arrival of the eigenfunctions at the arrival point at their corresponding eigenvalues and the consistent behavior of the extracted time of arrival distribution unambiguously identify the quantization of the classical first time of arrival as a first time of arrival operator. This points to a fundamental realization on how to quantize classical observables, not necessarily time observables, that are multiple valued.
Moreover, the idea behind the quantization discussed here can be extended to classical observables that are defined only in a limited region of the phase space, e.g. observables that take on complex values in some regions of the phase space. While classically the observable is defined in a limited region, we may find, as demonstrated by the harmonic oscillator, that the resulting quantized operator has a well defined meaning in the entire configuration space. The extension of the quantization process in the entire phase space can be understood from the fact that a quantum particle has the entire phase space available to it.
Open problem
We have investigated the time of arrival operator for the harmonic oscillator and for any continuous potential by coarse graining, that is by spatial confinement followed by successively increasing the confining length. It is desirable to directly investigate their properties in the Hilbert space ![]() without spatial confinement and to establish that their properties in the entire configuration space indeed emerges from the sequence of coarse grainings of the time of arrival operator. This has been done for the free time of arrival operator and remains to be done in the interacting case. The first step is to establish that the time of arrival operators are densely defined operators in the Hilbert space
without spatial confinement and to establish that their properties in the entire configuration space indeed emerges from the sequence of coarse grainings of the time of arrival operator. This has been done for the free time of arrival operator and remains to be done in the interacting case. The first step is to establish that the time of arrival operators are densely defined operators in the Hilbert space ![]() . You may start here. Contact us if you are interested in collaborating with us on this problem.
. You may start here. Contact us if you are interested in collaborating with us on this problem.
References
- E.A. Galapon, “Shouldn’t there be an antithesis to quantization?”, J. Math. Phys. 45, 3180 (2004).
- E.A. Galapon, R.F. Caballar, and R. Bahague, “Confined Quantum Time of Arrivals”, Phys. Rev. Lett. 93, 180406 (2004).
- E.A. Galapon, F. Delgado, J.G. Muga, and I. Egusquiza, “Transition from discrete to continuous time-of-arrival distribution for a quantum particle”, Phys. Rev. A 72, 042107 (2005).
- E.A. Galapon, “Theory of quantum arrival and spatial wave function collapse on the appearance of particle”, Proc. Roy. Soc. Lond. A 465 2101 (2009).