Is there a mass quantum operator?

$kg$
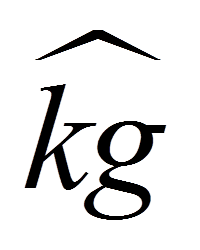
Yes, there is a mass operator in the same way there is a spin operator.

One of the central tenets of quantum mechanics is the one-to-one correspondence between what can be measured on a given system and an operator in the space of all possible states of the system. It asserts that to every quantity that you can measure there is a corresponding operator to it, the measurable values of the quantity being exactly the corresponding eigenvalues of the operator.

Since mass is a measurable property of a given particle, it is not unreasonable to expect that mass corresponds to a quantum operator. But there seems to be a snag against the idea of a mass operator—quantum observables have a distribution of values, the outcome of a measurement is determined by the wavefunction of the system. However, it appears from all our measurements that the mass, say of an electron, is a characteristic property of the electron. That is we measure the same value independent of the wavefunction of the electron.

The truth is mass can be perfectly accommodated within quantum mechanics as an operator. The observation that the same mass is measured independent of the wavefunction of the electron can be taken to mean that every wavefunction is an eigenfunction of the mass operator, with a corresponding eigenvalue equal to the measured mass. This implies that the mass operator $\widehat{\mathbf{m}}$ is proportional to the identity operator of the system, $\widehat{\mathbf{I}}$ , with the proportionality constant being the mass, $m_e$ . That is the mass operator is given by $\widehat{\mathbf{m}} = m_{e} \widehat{\mathbf{I}}$ . So for every wavefunction $\Psi$ the electron is in, we have $\widehat{\mathbf{m}} \Psi= m_e \widehat{\mathbf{I}}\Psi = m_e \Psi$ so that indeed every wavefunction $\Psi$ is an eigenfunction of $\widehat{\mathbf{m}}$ with the corresponding eigenvalue $m_e$ . Hence, in whatever wavefunction the electron is at, we will measure the same mass $m_e$ .

The above construction of the mass operator may appear contrived. But it is not. Let us consider the spin angular momentum of an electron. The spin angular momentum is given by

(1) $\begin{equation*} \vec{\mathbf{L}}=\frac{\hbar}{2} \sigma_x \hat{\mathbf{i}} + \frac{\hbar}{2} \sigma_y \hat{\mathbf{j}} + \frac{\hbar}{2} \sigma_z \hat{\mathbf{k}} \end{equation*}$

where $\sigma_x$ , $\sigma_y$ and $\sigma_z$ are the spin Pauli matrices. The magnitude of the angular is given by

(2) $\begin{equation*} \vec{\mathbf{L}}\cdot \vec{\mathbf{L}} = \frac{3}{4} \hbar^2 \mathbb{I} \end{equation*}$

where $\mathbb{I}$ is the $2 \times 2$ identity matrix. To arrive at the above expresssion, we have used the property of the Pauli matrices that their square is equal to the identity matrix.

The magnitude (square) of the angular momentum, $\vec{\mathbf{L}}\cdot \vec{\mathbf{L}}$ , is certainly an observable, a measurable property of the electron. But notice that it is proportional to the identity matrix, which means that all wavefunctions of the electron are eigenfunctions of the operator $\vec{\mathbf{L}}\cdot \vec{\mathbf{L}}$ , with the corresponding eigenvalue equal to the proportionality constant $3 \hbar^2/4$ . That is, in whatever wavefunction the electron is, we will always find the measured value of $\vec{\mathbf{L}}\cdot \vec{\mathbf{L}}$ to be $3\hbar^2/4$ . What this means is that the magnitude of the angular momentum of the electron is an intrinsic property that the electron posses, a property that is independent of the state of the electron and widely known as the spin.

In summary, every intrinsic property of a particle, a property that defines the particle itself, such as mass, charge and spin, is a quantum operator proportional to the identity operator with the proportionality constant equal to the measured value of the property. We can push further and say that the intrinsic observables of a particle are exactly those (hermitian) operators that commute with all the operators of the system. But since intrinsic observables commute with all other observables, they are as good as scalar (non-operator) quantities. It is for that reason that we can talk about them as if they are not operators at all.

Leave a Reply Cancel reply