In (Galapon 2017) we considered the problem of missing terms arising from evaluating the incomplete Stieltjes transform,
(1) ![]()
following from binomially expanding the kernel ![]() about
about ![]() and then integrating the resulting infinite series term by term. The interchange of summation and integration leads to the infinite series
and then integrating the resulting infinite series term by term. The interchange of summation and integration leads to the infinite series ![]() whose terms are divergent integrals. Assigning values to the (divergent) integrals by, say, analytic continuation yields a result that completely misses out a group of terms of the exact result. The problem of the missing terms was addressed in by lifting the integration in the complex plane.
whose terms are divergent integrals. Assigning values to the (divergent) integrals by, say, analytic continuation yields a result that completely misses out a group of terms of the exact result. The problem of the missing terms was addressed in by lifting the integration in the complex plane.
Under the sole assumption that the function ![]() possesses an analytic extension,
possesses an analytic extension, ![]() , in the interval
, in the interval ![]() , the incomplete Stieltjes integral assumes the evaluation
, the incomplete Stieltjes integral assumes the evaluation
(2) 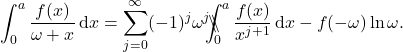
(3) 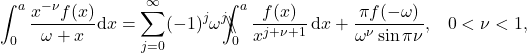
for all ![]() , where
, where ![]() is the nearest singularity of
is the nearest singularity of ![]() to the origin and
to the origin and ![]() is the finite part of the divergent integral
is the finite part of the divergent integral ![]() . For
. For ![]() , the finite parts are given by
, the finite parts are given by
(4) ![Rendered by QuickLaTeX.com \begin{equation*} \backslash\!\!\!\!\backslash\!\!\!\!\!\int_{0}^{a} \frac{f(x)}{x^{n+1}} \mathrm{d}x = \lim_{\epsilon\rightarrow 0^+}\left[\int_{\epsilon}^a \frac{f(x)}{x^{n+1}} -\sum_{k=0}^{n-1}\frac{f^{(k)}(0)}{k! (n-k)}\frac{1}{\epsilon^{n-k}} + \frac{f^{(n)}(0)}{n!}\ln \epsilon\right] , \end{equation*}](https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-8cccb53ac9a7a4ef1be8045e2c1dafc6_l3.png)
for all ![]() ; and for
; and for ![]() , the finite parts are
, the finite parts are
(5) ![Rendered by QuickLaTeX.com \begin{equation*} \backslash\!\!\!\!\backslash\!\!\!\!\!\int_{0}^{a} \frac{f(x)}{x^{m+\nu}} \mathrm{d}x = \lim_{\epsilon\rightarrow 0^+}\left[\int_{\epsilon}^{a}\frac{f(x)}{x^{m+\nu}}\mathrm{d}x - \sum_{j=0}^{m-1} \frac{f^{(j)}(0)}{j! (n+\nu-j-1)}\frac{1}{\epsilon^{n+\nu-j-1}}\right] \end{equation*}](https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-e8bd134fa7770adbc2ec6a91162cdc43_l3.png)
for all ![]() . The analyticity of
. The analyticity of ![]() at the origin guarantees the existence of the above limits.
at the origin guarantees the existence of the above limits.
The infinite series in equations \eqref{fpi1} and \eqref{fpi2} are the results of term by term integration with the divergent integrals assigned values equal to their finite parts, and the terms proportional to ![]() are the terms that would be missed out when the divergent integrals were merely replaced with their finite parts.
are the terms that would be missed out when the divergent integrals were merely replaced with their finite parts.
Now when the upper limit of integration is infinity, we obtain the well-known Stieltjes transform which is defined by the limit
(6) ![]()
It was tacitly claimed without proof in (Galapon 2017) that equations \eqref{stel1} and \eqref{stel2} hold for ![]() which is equivalent to interchanging the limit and the summation. This claim was demonstrated by three examples. Of course, it is not necessary that the result of a pair of sequence of operations is preserved by the interchange of the operations, and one can raise legitimately the possibility that the examples are mere coincidences. Here we give the explicit proof that indeed the interchange of the order of the summation and the limit is justified under the conditions stated there.
which is equivalent to interchanging the limit and the summation. This claim was demonstrated by three examples. Of course, it is not necessary that the result of a pair of sequence of operations is preserved by the interchange of the operations, and one can raise legitimately the possibility that the examples are mere coincidences. Here we give the explicit proof that indeed the interchange of the order of the summation and the limit is justified under the conditions stated there.
Proof of the legitimacy of the interchange
Under the above stated assumption on ![]() , the finite part integrals given by equations \eqref{fpi1} and \eqref{fpi2} have the fundamental property that they posses the following contour integral representations in the complex plane,
, the finite part integrals given by equations \eqref{fpi1} and \eqref{fpi2} have the fundamental property that they posses the following contour integral representations in the complex plane,
(7) ![]()
(8) ![]()
where ![]() and
and ![]() take the positive real axis as their branch cuts, and the contour
take the positive real axis as their branch cuts, and the contour ![]() is the contour straddling the cut starting from
is the contour straddling the cut starting from ![]() and ending at
and ending at ![]() itself, as depicted in Figure-1, with all singularities of
itself, as depicted in Figure-1, with all singularities of ![]() lying outside of
lying outside of ![]() .
.
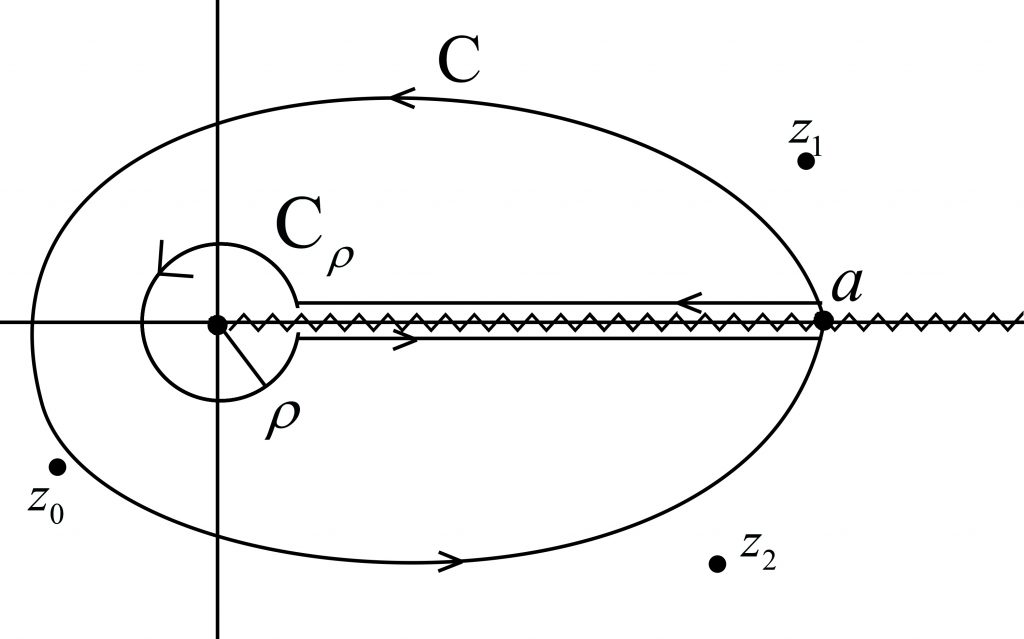
The contour ![]() in the contour integral representation of the finite part integrals. The points
in the contour integral representation of the finite part integrals. The points ![]() are the singularities of the analytic extension,
are the singularities of the analytic extension, ![]() , of
, of ![]() , and none of them is enclosed by
, and none of them is enclosed by ![]() .
. ![]() is the closest singularity to the origin.
is the closest singularity to the origin.
The integral representations \eqref{intergralrep1} and \eqref{integralrep2} were the keys to the evaluation of the Stieltjes integral in terms of the finite parts and to the recovery of the missing terms. And they, too, are the keys in establishing the validity of the interchange of the limit and summation. The proof will proceed in two steps. First is to show the existence of the limit of the finite part integral as ![]() under the assumption that the Stieltjes transform exists. And second is to show the uniform convergence of the infinite series in equations \eqref{stel1} and \eqref{stel2} for sufficiently large
under the assumption that the Stieltjes transform exists. And second is to show the uniform convergence of the infinite series in equations \eqref{stel1} and \eqref{stel2} for sufficiently large ![]() . Once uniform convergence is established, the validity of the interchange will follow from the well-known Dominated Convergence Theorem.
. Once uniform convergence is established, the validity of the interchange will follow from the well-known Dominated Convergence Theorem.
Case 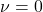
First let us establish the necessary condition for the existence of the limit of the finite part as ![]() . For some positive
. For some positive ![]() we deform the contour of integration
we deform the contour of integration ![]() in equation \eqref{intergralrep1} into the keyhole contour with the circular portion having the radius
in equation \eqref{intergralrep1} into the keyhole contour with the circular portion having the radius ![]() as shown in the Figure-1. Then along the deformed contour, the finite part assumes the form,
as shown in the Figure-1. Then along the deformed contour, the finite part assumes the form,
(9) ![]()
Since the first term is independent of ![]() , only the second term determines the behavior in the limit of arbitrarily large
, only the second term determines the behavior in the limit of arbitrarily large ![]() . Clearly the limit exists for all non-negative integer
. Clearly the limit exists for all non-negative integer ![]() when
when ![]() is integrable at infinity; but this is one condition to impose in order for the Stieltjes transform to exist. Hence under the assumption that the Stieltjes transform exists, the limit
is integrable at infinity; but this is one condition to impose in order for the Stieltjes transform to exist. Hence under the assumption that the Stieltjes transform exists, the limit
(10) ![]()
exists for all non-negative integer ![]() . (A similar consideration on the existence of the limit \eqref{fpilimit} has been made in (Tica&Galapon 2017), but the results there and here have a subtle difference. There the limit was considered without reference to the existence of the Stieltjes integral, in contrast to our intension here which is to show the existence of the limit when the Stieltjes transform exists.)
. (A similar consideration on the existence of the limit \eqref{fpilimit} has been made in (Tica&Galapon 2017), but the results there and here have a subtle difference. There the limit was considered without reference to the existence of the Stieltjes integral, in contrast to our intension here which is to show the existence of the limit when the Stieltjes transform exists.)
Now we show that the infinite series in the right hand side of equation \eqref{stel1} converges uniformly for sufficiently large ![]() . To accomplish this, we establish a bound for the finite part using equation \eqref{deformed1}. Let
. To accomplish this, we establish a bound for the finite part using equation \eqref{deformed1}. Let ![]() and
and ![]() be positive numbers such that
be positive numbers such that ![]() , where
, where ![]() is again the radius of the circle
is again the radius of the circle ![]() in Figure-1; moreover, let the upper limit of integration be
in Figure-1; moreover, let the upper limit of integration be ![]() . First let us bound the portion of the integral along the circular path
. First let us bound the portion of the integral along the circular path ![]() . Since
. Since ![]() is assumed to be analytic at the origin, it admits the expansion
is assumed to be analytic at the origin, it admits the expansion
(11) 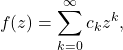
with a a radius of convergence ![]() . Substituting the parametrization
. Substituting the parametrization ![]() in the integral, we obtain
in the integral, we obtain
(12) 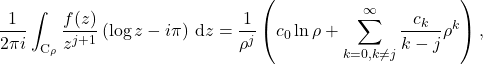
from which obtain the desired bound
(13) 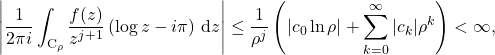
the right hand side being finite because ![]() is less than the radius of convergence of the infinite series. On the other hand, the second term has the finite bound
is less than the radius of convergence of the infinite series. On the other hand, the second term has the finite bound
(14) ![]()
following from the assumed existence of the Stieltjes transform. Combining the two bounds, the finite part has the bound
(15) 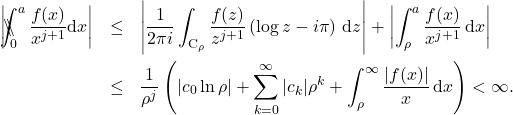
Observe that the right hand side is independent of ![]() for all
for all ![]() so that it is uniformly bounded for sufficiently large
so that it is uniformly bounded for sufficiently large ![]() .
.
We now establish the uniform convergence of the infinite series for all ![]() . The infinite series can be bounded as follows,
. The infinite series can be bounded as follows,
(16) 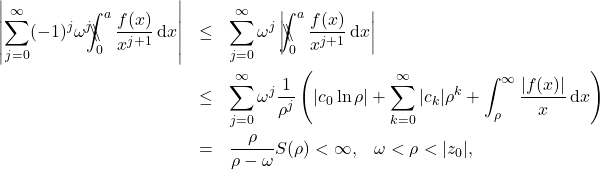
where ![]() is the quantity in brackets in the second line. Since for every fixed
is the quantity in brackets in the second line. Since for every fixed ![]() there exists a
there exists a ![]() such that
such that ![]() , inequality \eqref{inequality1} implies that the infinite series converges uniformly for a fixed
, inequality \eqref{inequality1} implies that the infinite series converges uniformly for a fixed ![]() for all
for all ![]() . Then we can interchange the order of limit and summation, and obtain the desired result,
. Then we can interchange the order of limit and summation, and obtain the desired result,
(17) 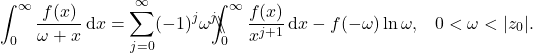
If it happens that the complex extension, ![]() , of
, of ![]() is entire so that
is entire so that ![]() , the series absolutely converges for all
, the series absolutely converges for all ![]() . The absolute convergence of the infinite series in equation \eqref{stel1limit} for positive
. The absolute convergence of the infinite series in equation \eqref{stel1limit} for positive ![]() extends the validity of equation \eqref{stel1limit} to complex arguments by analytic continuation. Equation \eqref{stel1limit} is valid for complex
extends the validity of equation \eqref{stel1limit} to complex arguments by analytic continuation. Equation \eqref{stel1limit} is valid for complex ![]() with
with ![]() , with
, with ![]() assuming its principal value.
assuming its principal value.
Case 
Now for the second case, the finite part integral assumes the form
(18) ![]()
after deformation of the contour ![]() to the keyhole contour as depicted again in Figure-1. In this form it is sufficient for
to the keyhole contour as depicted again in Figure-1. In this form it is sufficient for ![]() to be integrable at infinity in order for the limit as
to be integrable at infinity in order for the limit as ![]() to exist. Again this is the same condition for the Stieltjes transform to exist. So, under the existence of the Stieltjes transform, the limit exists.
to exist. Again this is the same condition for the Stieltjes transform to exist. So, under the existence of the Stieltjes transform, the limit exists.
We now show that the summation and the limit can be interchanged for ![]() in the same manner that we did above for
in the same manner that we did above for ![]() . Under similar conditions for
. Under similar conditions for ![]() ,
, ![]() and
and ![]() , we establish uniform convergence of the infinite series for sufficiently large
, we establish uniform convergence of the infinite series for sufficiently large ![]() . First, let us obtain a bound for the finite part integral for a given fixed finite
. First, let us obtain a bound for the finite part integral for a given fixed finite ![]() . For the first term of equation \eqref{branchexpand}, we have
. For the first term of equation \eqref{branchexpand}, we have
(19) 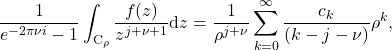
on substituting the expansion \eqref{expansion} back into the left hand side of equation \eqref{left}. From which we have the bound
(20) 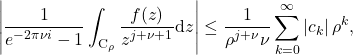
for ![]() . On the other hand, the second term has the bound,
. On the other hand, the second term has the bound,
(21) ![]()
Under the assumption that the Stieltjes transform exists, the most right hand side is finite. Combining the two bounds, we obtain the following bound for the finite part integral,
(22) 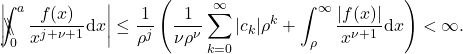
The right hand side is also independent of ![]() for all
for all ![]() so that the finite part for the present case is uniformly bounded for sufficiently large
so that the finite part for the present case is uniformly bounded for sufficiently large ![]() .
.
Given the inequality \eqref{bound2} for the finite part, we obtain the following bound for the infinite series,
(23) 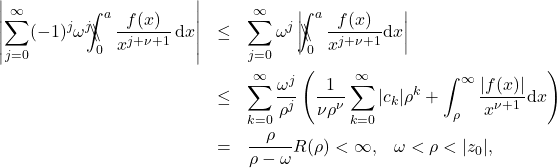
where ![]() is the quantity in parenthesis in the second line. Again the bound is independent of
is the quantity in parenthesis in the second line. Again the bound is independent of ![]() for all
for all ![]() so that the infinite sum is uniformly convergent for sufficiently large
so that the infinite sum is uniformly convergent for sufficiently large ![]() for every fixed
for every fixed ![]() . Then we can interchange the summation and limit to obtain the desired result,
. Then we can interchange the summation and limit to obtain the desired result,
(24) 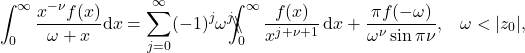
for ![]() . Again by analytic continuation the validity of equation \eqref{stel2limit} can be extended to complex
. Again by analytic continuation the validity of equation \eqref{stel2limit} can be extended to complex ![]() with
with ![]() and with
and with ![]() assuming its principal value.
assuming its principal value.