Abstract
Current quantum orthodoxy claims that the statistical collapse of the wave-function arises from the interaction of the measuring instrument with its environment through the phenomenon known as environment-induced decoherence. Here it is shown that there exists a measurement scheme that is exactly decohering without the aid of an environment. The scheme relies on the assumption that the meter is decomposable into probe and pointer, with the probe taken to be inaccessible for observation. Under the assumption that the probe and the pointer initial states are momentum limited, it is shown that coherences die out within a finite measurement time and the pointer states are exactly orthogonal after a sufficiently longer time of measurement. Furthermore, it is shown that the measurement scheme reproduces the main result of environment-induced decoherence theory that coherences decay asymptotically in time for a general initial state of the probe.
Download or purchase your copy of the paper here.
Download an earlier version of the paper here
Our everyday experience with measuring instruments registering unambiguous read-outs runs conflict with the unitary dynamics of quantum mechanics [1]. The quantum equation of motion, due to the unitarity of the Schrodinger equation, evolves an initial definite meter reading (say zero) to a linear superposition of all possible readings that are in correlation with the possible values of the property of the system being measured; this leaves the meter in a state without a definite reading, contrary to our experience. This comes about because the interaction of the meter and the system during measurement entangles them into an inseparable unit in a definite state–with neither the meter nor the system having a separate state of its own. Within the confines of standard quantum mechanics, the emergence of definite outcome from this entangled state is addressed by means of a process known as quantum decoherence. The environment-induced decoherence theory (EIDT) provides a mechanism for decoherence to occur [2-22]. It is anchored on the realization that the meter is not isolated from the environment; and it is the interaction between the environment and the meter that enforces decoherence. However, EIDT is being criticized for not being “a well-defined process” for the following reasons: (i) Suppression of coherences is approximate only; (ii) the induced pointer basis is only approximately orthogonal; (iii) it cannot accommodate isolated measuring instruments [3-26]. In this Letter we show the existence of a measurement scheme that exihibits exact quantum decoherence without the aid of an environment.
Given that an environment is defined as a quantum system with an arbitrarily large or infinite number of unobservable degrees of freedom, in this paper we address the question: With the system and the meter interacting in the (finite) time interval ![]() , after which the meter is decoupled from the system, is there a measurement scheme, not involving an environment, such that right after
, after which the meter is decoupled from the system, is there a measurement scheme, not involving an environment, such that right after ![]() the system and the meter-pointer are exactly decohered into a classical mixed state with the pointer states mutually orthogonal? By “exactly decohered” we mean that the relevant coherences are identically zero right after
the system and the meter-pointer are exactly decohered into a classical mixed state with the pointer states mutually orthogonal? By “exactly decohered” we mean that the relevant coherences are identically zero right after ![]() . Here it is shown that exact decoherence can be achieved within
. Here it is shown that exact decoherence can be achieved within ![]() without an environment, relying only on the assumption that the meter has to be decomposed into probe and pointer, with the probe taken to be inaccessible for observation and prepared in an initial momentum limited state. Moreover, it is shown that, under similar condition on the initial state of the pointer, the pointer-states are exactly orthogonal. Explicit expressions are obtained for the decoherence and orthogonality times are obtained. Furthermore, it is shown that that the measurement scheme reproduces the typical EIDT asymptotic decay in time of coherences for a general initial state of the probe. These results lead to the unexpected fundamental result that exact quantum decoherence can be achieved through an internal one degree of freedom within finite measurement interaction time.
without an environment, relying only on the assumption that the meter has to be decomposed into probe and pointer, with the probe taken to be inaccessible for observation and prepared in an initial momentum limited state. Moreover, it is shown that, under similar condition on the initial state of the pointer, the pointer-states are exactly orthogonal. Explicit expressions are obtained for the decoherence and orthogonality times are obtained. Furthermore, it is shown that that the measurement scheme reproduces the typical EIDT asymptotic decay in time of coherences for a general initial state of the probe. These results lead to the unexpected fundamental result that exact quantum decoherence can be achieved through an internal one degree of freedom within finite measurement interaction time.
In general the state of a quantum system is described in terms of the density matrix to accommodate both pure and mixed states. Pure states satisfy the superposition principle, and they are characterized by the existence of a measurement whose outcome is predictable with certainty. On the other hand, mixed states are weighted superpositions of pure states, and they are characterized by the absence of measurement whose outcome is predictable. Quantum interference of mutually exclusive outcomes are manifested by the off-diagonal elements—the coherences—of the density matrix. Full coherence is the hallmark of pure states, and degraded coherence is that of mixed states. An extreme class of states constitutes those that lack coherences at all, i.e. diagonal mixed states. For such states, probabilities computed from them satisfy the classical rules of probability, and hence may be consistently interpreted as classical states admitting ignorance interpretation. Now the eventual disappearance of the coherences of a pure state while leaving the diagonal of the corresponding density matrix intact is referred to as decoherence. Any decoherence process then maps a pure quantum state into a mixed classical state. Such a process cannot be unitary, because unitary dynamics maps a pure state into another pure state.
However, a non-unitary evolution can be achieved from the unitary Schrodinger equation by entangling the system with another system through a unitary interaction, and then ignoring the auxiliary system. Entanglement allows information to leak out of the system and ignoring the auxiliary system leaves the system in a mixed state. In environment-induced decoherence theory, the measuring instrument is immersed in an environment. Decoherence is accomplished by tracing out the environment, leaving the system and the measuring instrument in a mixed state. In this paper, our approach is to endow the measuring instrument an inaccessible internal degree of freedom which does not play a direct role in the registration of measurement outcome but nevertheless is capable of dispersing quantum correlations.
Here we will consider the measurement of a non-degenerate observable ![]() , with eigenvalues
, with eigenvalues ![]() and eigenvectors
and eigenvectors ![]() , of a finite dimensional quantum system
, of a finite dimensional quantum system ![]() . The key to our treatment is the realization that the measuring instrument has to be decomposed in two parts: the probe and the pointer. In orthodox quantum mechanics, these two parts are lumped into one system. The entire Hilbert space comprising the measurement scheme is then
. The key to our treatment is the realization that the measuring instrument has to be decomposed in two parts: the probe and the pointer. In orthodox quantum mechanics, these two parts are lumped into one system. The entire Hilbert space comprising the measurement scheme is then ![]() , where
, where ![]() is the system Hilbert space,
is the system Hilbert space, ![]() is the probe Hilbert space, and
is the probe Hilbert space, and ![]() is the pointer Hilbert space. We will find it necessary that the probe and pointer Hilbert spaces are infinite dimensional. The constraints on the infinite dimensionalities of the probe and pointer Hilbert spaces will be demonstrated as necessary to achieve exact reduction and the existence of a projection-valued measure pointer observable. Incidentally, the infinite dimensionality of the pointer Hilbert space will accommodate any dimensionality of the system, so that the measuring instrument works for all systems.
is the pointer Hilbert space. We will find it necessary that the probe and pointer Hilbert spaces are infinite dimensional. The constraints on the infinite dimensionalities of the probe and pointer Hilbert spaces will be demonstrated as necessary to achieve exact reduction and the existence of a projection-valued measure pointer observable. Incidentally, the infinite dimensionality of the pointer Hilbert space will accommodate any dimensionality of the system, so that the measuring instrument works for all systems.
We assume a measurement model similar to that of Von-Neumann’s scheme with the measurement Hamiltonian
(1) ![]()
where ![]() and
and ![]() are the respective position and momentum operators of the probe, and
are the respective position and momentum operators of the probe, and ![]() and
and ![]() are real coupling constants which we take to be arbitrary at the moment;
are real coupling constants which we take to be arbitrary at the moment; ![]() is the observable to be measured and
is the observable to be measured and ![]() is a pointer observable;
is a pointer observable; ![]() has a compact support in the time interval
has a compact support in the time interval ![]() . For simplicity, we take
. For simplicity, we take ![]() to be a square pulse of height
to be a square pulse of height ![]() (see appendix for further discussion on this assumption). The necessity of the infinite dimensionality of the probe Hilbert space is made clear by the introduction of the position
(see appendix for further discussion on this assumption). The necessity of the infinite dimensionality of the probe Hilbert space is made clear by the introduction of the position ![]() and momentum
and momentum ![]() operators in the Hamiltonian. Notice that there is no direct coupling between the system and the pointer in the Hamiltonian. Their interaction is mediated through the probe.
operators in the Hamiltonian. Notice that there is no direct coupling between the system and the pointer in the Hamiltonian. Their interaction is mediated through the probe.
We take the initial state of the combined system to be the pure product state ![]() , where
, where ![]() ,
, ![]() ,
, ![]() are the initial states of the system, probe and pointer, respectively. Then the state after the measurement is
are the initial states of the system, probe and pointer, respectively. Then the state after the measurement is
(2) ![]()
where the unitary time evolution operator ![]() is given by
is given by
(3) ![]()
Note that the state ![]() in \eqref{fin} persists even after the interaction.
in \eqref{fin} persists even after the interaction.
To unravel the physical content of the final state, the evolution operator \eqref{evo} is factored in the form
(4) 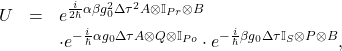
where we have used the commutation relation ![]() to obtain this result. With the obvious correspondences, we write
to obtain this result. With the obvious correspondences, we write ![]() . In this form we find that the total evolution is equivalent to a compound action, with the system-pointer interaction explicitly emerging. We now chose
. In this form we find that the total evolution is equivalent to a compound action, with the system-pointer interaction explicitly emerging. We now chose ![]() in such a way that the induced coupling of
in such a way that the induced coupling of ![]() and
and ![]() in
in ![]() is independent of the coupling of
is independent of the coupling of ![]() and
and ![]() to the probe, in particular,
to the probe, in particular, ![]() , where
, where ![]() is now the coupling constant between
is now the coupling constant between ![]() and
and ![]() , and is independent of
, and is independent of ![]() . We now likewise impose that
. We now likewise impose that ![]() .
.
Since the probe is just there to mediate the interaction between the system and the pointer and since we do not observe it, we trace it out to obtain the reduced density matrix for the combined system and pointer,
(5) ![]()
where ![]() is now simply given by
is now simply given by ![]() and
and
(6) ![]()
Due to the entanglement of the system and the pointer with the probe, the state ![]() is necessarily mixed.
is necessarily mixed.
Equation \eqref{ke} shows that the evolution of the system and the pointer can be effectively and conveniently described as a two-stage process. First is the non-unitary evolution of the initial pure state, ![]() , of the system and the pointer into the mixed state
, of the system and the pointer into the mixed state ![]() . Second is the unitary evolution of the mixed state
. Second is the unitary evolution of the mixed state ![]() into the mixed state
into the mixed state ![]() . The first stage is where decoherence must occur, the evolution being non-unitary; and the final establishment of the correlation between the eigenstates of the observable
. The first stage is where decoherence must occur, the evolution being non-unitary; and the final establishment of the correlation between the eigenstates of the observable ![]() and the pointer states must occur in the second stage.
and the pointer states must occur in the second stage.
One may point out that the probe by itself is an environment of the system and the pointer so that we have not really eliminated the role of an environment. True but the definition of environment in EIDT is a quantum system with an inaccessible infinite number of degrees of freedom which excludes the probe because it consists only of one degree of freedom. What the probe does is to assume the role of the environment only that it does not possess an infinite number of degrees of freedom.
Now expression (\eqref{keke}) holds for all pointer observables, but we now require ![]() to posses a simple spectrum spanning the real line, e.g. position or momentum operator. This requirement implies that
to posses a simple spectrum spanning the real line, e.g. position or momentum operator. This requirement implies that ![]() is necessarily unbounded and that the Hilbert space of the pointer is necessarily infinite dimensional. We see later the necessity of this requirement on
is necessarily unbounded and that the Hilbert space of the pointer is necessarily infinite dimensional. We see later the necessity of this requirement on ![]() . Let
. Let ![]() and
and ![]() be the generalized eigenvectors of
be the generalized eigenvectors of ![]() and
and ![]() , respectively. Then
, respectively. Then
(7) 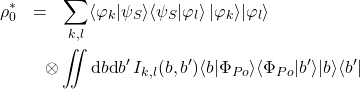
(8) 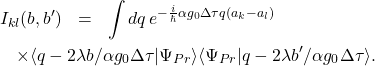
The density matrix ![]() is manifestly mixed. Clearly if decoherence is to occur in the desired measurement basis, the coherences of
is manifestly mixed. Clearly if decoherence is to occur in the desired measurement basis, the coherences of ![]() , the off-diagonal elements, must identically vanish and this requires vanishing of the functions
, the off-diagonal elements, must identically vanish and this requires vanishing of the functions ![]() for
for ![]() (which we will shorten as
(which we will shorten as ![]() ).
).
The expression for ![]() is a Fourier transform in the parameter
is a Fourier transform in the parameter ![]() ; and it is a well-known theorem that the Fourier transform vanishes as its parameter approaches infinity. This provides a mechanism for the disappearance of the coherences. In the limit, the reduced density matrix of the system and the pointer becomes
; and it is a well-known theorem that the Fourier transform vanishes as its parameter approaches infinity. This provides a mechanism for the disappearance of the coherences. In the limit, the reduced density matrix of the system and the pointer becomes
(9) ![]()
where ![]() . The reduction from the pure product state of the system and the pointer to the mixed correlated state \eqref{von} was postulated by von Neumann \cite{von}. Here we find that the reduction arises naturally from our model in the limit of infinite
. The reduction from the pure product state of the system and the pointer to the mixed correlated state \eqref{von} was postulated by von Neumann \cite{von}. Here we find that the reduction arises naturally from our model in the limit of infinite ![]() .
.
More important is that the objective of EIDT to induce decoherence can already be achieved in our model using only a one-degree of freedom to disperse correlations between the system and the pointer. In particular, for fixed interaction strength and coupling coefficient, the coherences vanishes asymptotically with the interaction time ![]() . We can appreciate this further by looking at the specific case where the probe is prepared initially in a harmonic oscillator ground state,
. We can appreciate this further by looking at the specific case where the probe is prepared initially in a harmonic oscillator ground state, ![]() . For this case, we have
. For this case, we have ![]() , where
, where ![]() is independent of
is independent of ![]() . For fixed
. For fixed ![]() and
and ![]() , we recover the typical exponential suppression in time of the coherences observed in EIDT, so that for an arbitrarily long time the coherences are, for all practical purposes, zero and decoherence is achieved. But this suffers from the criticism that the loss of coherence is only approximate.
, we recover the typical exponential suppression in time of the coherences observed in EIDT, so that for an arbitrarily long time the coherences are, for all practical purposes, zero and decoherence is achieved. But this suffers from the criticism that the loss of coherence is only approximate.
So we now tackle the question whether there exists a condition under which coherences vanish for finite ![]() , i.e for finite
, i.e for finite ![]() ,
, ![]() and
and ![]() . We now show that exact decoherence occurs for fixed
. We now show that exact decoherence occurs for fixed ![]() under the condition that the \textcolor{red}{initial} probe wave function,
under the condition that the \textcolor{red}{initial} probe wave function, ![]() , is momentum limited: A wave-function
, is momentum limited: A wave-function ![]() in
in ![]() is momentum limited if
is momentum limited if ![]() for some
for some ![]() . It is known that such a function has an extension
. It is known that such a function has an extension ![]() (obtained by replacing the real parameter
(obtained by replacing the real parameter ![]() in
in ![]() with the complex variable
with the complex variable ![]() ) in the complex plane that is both entire and exponential of type
) in the complex plane that is both entire and exponential of type ![]() [28]. Central to the vanishing of the coherences at finite
[28]. Central to the vanishing of the coherences at finite ![]() is the following result.
is the following result.
Lemma
Let
be entire and exponential of type
, and
; then
for all
.
An example of a wave-function in ![]() that satisfies all the conditions of the Lemma is
that satisfies all the conditions of the Lemma is ![]() for some wave-number
for some wave-number ![]() . The complex extension,
. The complex extension, ![]() , of this wave-function is entire and of exponential of type
, of this wave-function is entire and of exponential of type ![]() .
.
Now let the probe wave-function ![]() be momentum limited so that its complex extension is exponential of type
be momentum limited so that its complex extension is exponential of type ![]() . Then the function
. Then the function ![]() in equation \eqref{bebebe} is itself entire and exponential of type
in equation \eqref{bebebe} is itself entire and exponential of type ![]() (see appendix). By the Lemma we have
(see appendix). By the Lemma we have ![]() for all (finite)
for all (finite) ![]() . Define
. Define ![]() . Then the functions
. Then the functions ![]() vanish under the condition
vanish under the condition
(10) ![]()
for all ![]() and
and ![]() . Under this condition, the reduced density matrix of the system and the pointer assumes the form
. Under this condition, the reduced density matrix of the system and the pointer assumes the form
(11) ![]()
where
(12) ![]()
with ![]() . Notice that
. Notice that ![]() is independent of
is independent of ![]() so that the reduced density matrix \eqref{prereduced} is a product state, with the system’s density matrix completely decohered in the desired basis and the pointer now in a mixed state. At this point in the measurement, the system and the pointer have become uncorrelated.
so that the reduced density matrix \eqref{prereduced} is a product state, with the system’s density matrix completely decohered in the desired basis and the pointer now in a mixed state. At this point in the measurement, the system and the pointer have become uncorrelated.
In the second stage of the measurement, the unitary operator acts to establish the correlation between the system and the pointer. Substituting equation \eqref{prereduced} back into equation \eqref{ke}, we obtain the full reduced density matrix of the system and the pointer,
(13) ![]()
where the ![]() ‘s are given by
‘s are given by
(14) ![]()
In \eqref{reduced} perfect correlation has been established between the eigenstates, ![]() , of
, of ![]() and the set of states,
and the set of states, ![]() , of the pointer. The states
, of the pointer. The states ![]() ‘s then constitute the pointer states. These pointer states are different from the pointer states in the von Neumann model, which are the
‘s then constitute the pointer states. These pointer states are different from the pointer states in the von Neumann model, which are the ![]() ‘s.
‘s.
Our ability to obtain unambiguous outcomes depends on the mutual orthogonality of the pointer states. We now show that under similar conditions as above the ![]() ‘s are pairwise orthogonal. For
‘s are pairwise orthogonal. For ![]() we have
we have
(15) 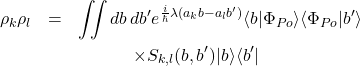
(16) 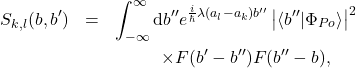
in which ![]() .
. ![]() and
and ![]() are orthogonal if
are orthogonal if ![]() for all
for all ![]() . To avoid unnecessary complications, we can assume that
. To avoid unnecessary complications, we can assume that ![]() is real and even, i.e.
is real and even, i.e. ![]() . This requires that
. This requires that ![]() is real and with definite parity.
is real and with definite parity.
By the same reasoning above, we can make ![]() vanish by imposing that
vanish by imposing that ![]() is momentum limited of some type
is momentum limited of some type ![]() , which we assume to be real as well. Now
, which we assume to be real as well. Now ![]() is exponential of type
is exponential of type ![]() . By the Lemma the integral vanishes when
. By the Lemma the integral vanishes when ![]() . Since
. Since ![]() is positive, the condition implies that the coupling constant
is positive, the condition implies that the coupling constant ![]() cannot be arbitrary but must satisfy the condition
cannot be arbitrary but must satisfy the condition
(17) ![]()
Then for all ![]() and
and ![]() ,
, ![]() , orthogonality is achieved under the condition
, orthogonality is achieved under the condition
(18) ![]()
together with equation (\eqref{pe}). The orthogonality of the pointer states implies that we can associate them with a projection valued observable of the pointer.
We now look closer into the conditions for decoherence and orthogonality. The right-hand side of the inequality \eqref{decond} naturally defines the time scale
(19) ![]()
Thus for fixed ![]() ,
, ![]() ,
, ![]() and
and ![]() , the decoherence condition reduces to the condition
, the decoherence condition reduces to the condition
(20) ![]()
Then ![]() is naturally interpreted as the decoherence time, the minimum required time of observation for the measurement to induce exact decoherence. Thus for all finite parameters of the measurement, we achieve the statistical collapse of the density matrix within a finite time interval of measurement.
is naturally interpreted as the decoherence time, the minimum required time of observation for the measurement to induce exact decoherence. Thus for all finite parameters of the measurement, we achieve the statistical collapse of the density matrix within a finite time interval of measurement.
On the other hand, the right hand side of inequality \eqref{orcond} also defines the time scale
(21) ![]()
so that for finite and fixed coupling parameters the orthogonality condition reduces to
(22) ![]()
The time ![]() is the minimum required measurement time for the pointer states to become mutually orthogonal, which we refer to as the orthogonality time. Comparing the decoherence and orthogonality times, we find that
is the minimum required measurement time for the pointer states to become mutually orthogonal, which we refer to as the orthogonality time. Comparing the decoherence and orthogonality times, we find that
(23) ![]()
Hence for ![]() there is ambiguity on the measurement reading as the pointer states are not orthogonal even though complete decoherence has already occurred. Due to the inequality \eqref{ineq} it is sufficient to satisfy the orthogonality time condition to be satisfied in order to have an ambiguous outcome.
there is ambiguity on the measurement reading as the pointer states are not orthogonal even though complete decoherence has already occurred. Due to the inequality \eqref{ineq} it is sufficient to satisfy the orthogonality time condition to be satisfied in order to have an ambiguous outcome.
We now have a complete picture of the entire measurement process. The system and the pointer, together with the probe, start out in uncorrelated state. At ![]() the probe is coupled to the system and the pointer, bringing the system and the pointer with the probe in an entangled state. For interaction time
the probe is coupled to the system and the pointer, bringing the system and the pointer with the probe in an entangled state. For interaction time ![]() less than the decoherence time
less than the decoherence time ![]() , the system and the pointer remain entangled until the decoherence time is reached at which the entanglement vanishes and the system and the pointer are left in a separable correlated state. For a measurement time longer than the orthogonality time, the pointer is left in a set of mutually distinguishable set of states.
, the system and the pointer remain entangled until the decoherence time is reached at which the entanglement vanishes and the system and the pointer are left in a separable correlated state. For a measurement time longer than the orthogonality time, the pointer is left in a set of mutually distinguishable set of states.
Now it is known that recurrence arises in a system with a finite degree of freedom. It is for this reason that a quantum environment is required to have an infinite number of degrees of freedom to avoid recurrences. This can be raised against the current model as it has a finite number of component systems. However, this argument does not hold because the interaction is turned off after a finite duration of time. While the system and pointer are together coupled to the probe, information leaks out into the probe. After a sufficiently long time, all the information carried by the coherences has been transferred to the probe and this occurs at the decoherence time ![]() . At this time the probe is disconnected to the system and the pointer, so that there is no opportunity for the information that leaked out to return to execute quantum recurrence.
. At this time the probe is disconnected to the system and the pointer, so that there is no opportunity for the information that leaked out to return to execute quantum recurrence.
Thus we have shown the existence of a measurement scheme that accomplishes the goal of environment-induced decoherence theory without the aid of an environment. However, our result should not be construed as invalidating EIDT. While we have pointed out the problems of EIDT with regards to the asymptotic nature of decoherence and the non-orthogonality of the pointer states there, our example above with the harmonic oscillator ground state as an initial state shows that the exponential suppression of coherences occurs because of the choice of the initial state but a proper choice of the initial state yielded exact decoherence and orthogonal pointer states. It is a distinct possibility that a closer examination of the current models of EIDT may yield exact decoherence as well. Then our result here points a way into addressing the first two criticisms against EIDT. However, the third criticism, that EIDT cannot accommodate an isolated measuring instrument, still stands. But here we have shown that an environment is not necessary for decoherence to occur so that an isolated measuring instrument may exhibit decoherence effects. Our result here can then be seen as partly completing the program of quantum decoherence theory, with EIDT seen now only as another part, describing what happens in the presence of an environment, and not the entire story of quantum decoherence.
Appendix
Measurement dynamics: Let ![]() be a time dependent Hamiltonian that commutes at different times, i.e.
be a time dependent Hamiltonian that commutes at different times, i.e. ![]() for all
for all ![]() . Then the solution to the Schr\”{o}dinger equation is given by
. Then the solution to the Schr\”{o}dinger equation is given by
(24) ![]()
Quantum measurement is modeled by this kind of Hamiltonian, in particular, of the form ![]() , where
, where ![]() is a time independent operator and
is a time independent operator and ![]() is a real valued function that has a compact support in some time interval
is a real valued function that has a compact support in some time interval ![]() , so that
, so that ![]() is the duration of the measurement process. Then the state of the system right after the measurement is given by
is the duration of the measurement process. Then the state of the system right after the measurement is given by
(25) ![]()
where ![]() is the value of
is the value of ![]() at some point
at some point ![]() in the interval
in the interval ![]() (
(![]() by the mean value theorem). There are two situations at which this relation holds: First, is when the free Hamiltonian of the systems involved are zero; and second is when
by the mean value theorem). There are two situations at which this relation holds: First, is when the free Hamiltonian of the systems involved are zero; and second is when ![]() is much smaller than any relevant time scales of the free systems involved. The last one is true in particular when the measurement is impulsive. However, the former is the usual model in quantum measurements.
is much smaller than any relevant time scales of the free systems involved. The last one is true in particular when the measurement is impulsive. However, the former is the usual model in quantum measurements.
The interaction in the text corresponds to ![]() . For the general case of time-dependent
. For the general case of time-dependent ![]() , the entire result of the paper can be applied by replacing
, the entire result of the paper can be applied by replacing ![]() with
with ![]() using the mean value theorem. Thus while the assumption of a square pulse interaction appears limiting, it is in fact a simplifying assumption that can be applied to the general case.
using the mean value theorem. Thus while the assumption of a square pulse interaction appears limiting, it is in fact a simplifying assumption that can be applied to the general case.
Entire and exponential type functions: A complex valued function ![]() is called entire if its series expansion has an infinite radius of convergence; and
is called entire if its series expansion has an infinite radius of convergence; and ![]() is exponential of type
is exponential of type ![]() if, for sufficiently large
if, for sufficiently large ![]() , we have the asymptotic inequality
, we have the asymptotic inequality ![]() . Relevant to the present paper is the well-known Paley-Wiener Theorem: The entire function
. Relevant to the present paper is the well-known Paley-Wiener Theorem: The entire function ![]() is of exponential type
is of exponential type ![]() and belongs to
and belongs to ![]() in the real axis if and only if
in the real axis if and only if ![]() , where
, where ![]() \cite{boas}. If
\cite{boas}. If ![]() is entire and exponential of type
is entire and exponential of type ![]() and its restriction in the real line,
and its restriction in the real line, ![]() , is square integrable, then, from the Paley-Wiener theorem, the function
, is square integrable, then, from the Paley-Wiener theorem, the function ![]() is entire and exponential of type
is entire and exponential of type ![]() for every real
for every real ![]() .
.
Product of two exponential type functions: Let ![]() and
and ![]() be exponential functions of types
be exponential functions of types ![]() and
and ![]() , respectively, whose restrictions in the real line,
, respectively, whose restrictions in the real line, ![]() and
and ![]() , are vectors of
, are vectors of ![]() . Then they can be written as
. Then they can be written as ![]() and
and ![]() , so that
, so that ![]() , where
, where ![]() . Hence
. Hence ![]() is exponential of type
is exponential of type ![]() .
.
Proof of the Lemma: For ![]() perform the contour integration
perform the contour integration ![]() around the rectangle with vertices at
around the rectangle with vertices at ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; and then take the limit as
; and then take the limit as ![]() . If
. If ![]() is exponential of type
is exponential of type ![]() and if
and if ![]() , it is known that
, it is known that ![]() [28]. Under this condition, the integral along the edges parallel to the complex axis will vanish in the said limit. Since
[28]. Under this condition, the integral along the edges parallel to the complex axis will vanish in the said limit. Since ![]() is entire, it has no pole so that we have the equality
is entire, it has no pole so that we have the equality ![]() for all
for all ![]() . From this follows the inequality
. From this follows the inequality ![]() . The right hand side of the inequality can be made arbitrarily small by making
. The right hand side of the inequality can be made arbitrarily small by making ![]() arbitrarily large. This implies that the integral vanishes. For
arbitrarily large. This implies that the integral vanishes. For ![]() close the contour in the lower half plane to obtain the same result.
close the contour in the lower half plane to obtain the same result.
References
- P. Busch, P.J. Lahti, P. Mittelstaedt The Quantum Measurement Theory 2nd Ed. Springer-Verlag Berlin Heidelberg (1996).
- H.D. Zeh Found. Phys. 1, 69 (1970).
- H.D. Zeh Found. Phys. 3, 109 (1973).
- W.H. Zurek Phys. Rev. D 24, 1516 (1981).
- W.H. Zurek Phys. Rev. D 26, 1862 (1982).
- W.H. Zurek Rev. Mod. Phys. 75 715-775 (2003).
- M. Schlosshauer Rev. Mod. Phys. 76, 1267-1305 (2004).
- K. Camilleri Studies in History and Philosophy of Modern Physics 40, 290-302 (2009).
- A.O. Caldeira and A.J. Legget Phys. Rev. Lett. 46, 211-214 (1981).
- E. Joos, et al., Decoherence and the appearance of a classical world in quantum theory (2nd Ed) Springer, Berlin, New York, (2003).
- M. Schlosshauer Decoherence and the quantum to classical transition (Springer Verlag, Berlin Heidelberg, 2007).
- W.H. Zurek Nature Physics 5, 181-188 (2009).
- Riedel, C. J. and Zurek, W. H., Phys. Rev. Lett. 105, 020404 (2010).
- Blume-Kohout, R. and Zurek, W. H. Phys. Rev. A 73, 062310 (2006).
- C.J. Myatt Nature 403, 269-273 (2000).
- Y. Glickman, S. Kotler, N. Akerman and R. Ozeri Science 339 (6124), 1187 (2013).
- M. Brune et. al., Phys. Rev. Lett. 77, 4887-4890 (1996).
- P.G. Kwiat, A.J. Berglund, J.B. Altepeter and A.G. White Science 290, 498-501 (2000).
- X. Maitre et.al. J. Mod. Opt. 44, 2023-2032 (1997).
- M.B. Plenio and P.L. Knight Proc. Roy. Soc. A 453, 2017-2041 (1997).
- I.L. Chuang et.al. Science 270, 1633-1635 (1995).
- L. Viola J. Mod. Opt. 51 (16-18), 2357-2367 (2004).
- O.J. Pessoa Synthese 113, 323–346 (1998).
- L. Ballentine Foundations of Physics 38, 916–922 (2008).
- S. Tanona Synthese 190, 3625-3649 (2013).
- D. Wallace Philosophical Transactions of the Royal Society A 370 4576-4593 (2012).
- J. von Neumann Mathematical Foundations of Quantum Mechanics (Princeton University Press, Princeton, 1955).
- R.P.J. Boas Entire Functions (Academic Press Inc., Publishers, New York, N.Y., 1954).
Congrats Sir!
Thanks.