Integration by analytic extension

Let us consider two complex valued analytic functions, $g_1(z)$ and $g_2(z)$ , with respective domains, $D_1$ and $D_2$ . That a function is analytic means that it is differentiable in its domain except perhaps at some isolated points, such at poles. Let us suppose that the domains of the functions have non-trivial intersection, $D_{12}=D_1\cap D_2\neq \emptyset$ , which is open. If it happens that the functions are equal in their common domain,

(1) $\begin{equation*} g_1(z)=g_2(z),\;\;\; \mbox{for all}\; z\in D_1\cap D_2, \end{equation*}$

then the functions are known as analytic extensions of each other. In particular, $g_2(z)$ is the analytic extension of $g_1(z)$ in the rest of the domain of $g_2(z)$ ; and $g_1(z)$ is the analytic extension of $g_2(z)$ in the rest of the domain of $g_1(z)$ .

In certain applications, like in the evaluation of divergent integrals, analytic extension theory is used to assign values to functions outside their domains. So, for example, one can use $g_1(z)$ to compute the value of the function $g_2(z)$ for $z$ ‘s outside $D_2$ but falling in $D_1$ , and vice versa. However, that is not the application we have in mind in this post.

What we have in mind is the following. Let us say we are given two analytic functions $f_1(z)$ and $f_2(z)$ with intersecting domains, $D_1$ and $D_2$ , with the intersection given by $D_{12}=D_1\cap D_2$ . Let us say that the functional forms of the functions are so different that it is not immediately clear whether they are equal in their common domain or not. But let us say that we have established that there exists a segment, $\Gamma$ , contained in $D_{12}$ , such that the functions are equal there, $f_1(z)=f_2(z)$ for all $z\in \Gamma\subset D_{12}$ .

The question relevant to us in this post is Given the information on the equality of the functions on the segment, what can we conclude on the values of the functions on their common domain? Analytic extension theory says that equality of two analytic functions on a segment contained in their common domain implies their equality in the rest of their common domain. Explicitly

(2) $\begin{equation*} f_1(z)=f_2(z),\;\mbox{for all}\; z\in \Gamma \subset D_1\cap D_2 \; \Rightarrow\; f_1(z)=f_2(z),\; \mbox{for all}\; z\in D_1\cap D_2 . \nonumber \end{equation*}$

This is a powerful result that is a must learn for every student of mathematical physics.

$(a) Two analytic functions, <img loading=$ and $f_2(z), with respective domains,$ D_1 $and$ D_2 $, with a common domain,$ D_{12} $. (b) If the two functions are equal on the red segment$ \Gamma $, then they are equal in the entire region$ D_12 $." width="3216" height="1221" class="size-full wp-image-897" /></a> (a) Two analytic functions,$ f_1(z) $and$ f_2(z) $, with respective domains,$ D_1 $and$ D_2 $, and with a common domain,$ D_{12} $. (b) If the two functions are equal on the red segment,$ \Gamma $, then they are equal in the entire region$ D_{12}

$.[/caption] In this post, I wish to demonstrate the power and utility of analytic extension theory in integration. Let us consider a specific example. Let us say we given the function defined by the integral <a name="id4106636575"></a> (3) <img src="https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-3f289cc9c9b91073567290eccadd2d3c_l3.png" height="41" width="187" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{equation*} F(z)=\int_0^{\infty} f(t) \mathrm{e}^{-z t^2}\, \mathrm{d}t, \end{equation*}" title="Rendered by QuickLaTeX.com"/>where$

f(t) $is bounded so that the the integral converges absolutely when$ \mathrm{Re}(z)>0 $. Then the domain of$ F(z) $consists of the right-half of the complex plane,$ D=\{z\in\mathbb{C}| \mathrm{Re}(z)>0\} $. Let us now assume that we have already evaluated the integral in equation \eqref{integ} in terms of elementary or special functions. We now use analytic extension theory to generate new integrals out of the integral$ F(z) $in equation \eqref{integ}. Let$ z=x+ i y $, where$ x>0 $and$ y\in\mathbb{R}

$. Then (4) <img src="https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-c51d65952491c992008c5486a2cf80bf_l3.png" height="113" width="525" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{eqnarray*} F(x+iy)&= &\int_{0}^{\infty} f(t) \mathrm{e}^{-(x+i y) t^2}\, \mathrm{d}t\nonumber\\ &=&\int_0^{\infty} f(t) \mathrm{e}^{-x t^2}\cos(yt^2)\, \mathrm{d}t + i \int_0^{\infty} f(t) \mathrm{e}^{-x t^2}\sin(yt^2)\, \mathrm{d}t \nonumber \\ &=& F_c(x,y) + i F_s(x,y) \end{eqnarray*}" title="Rendered by QuickLaTeX.com"/>where <a name="id3167911692"></a> (5) <img src="https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-8e6d1ec9d5d578efcac6faaf64396e22_l3.png" height="41" width="275" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{equation*} F_c(x,y)=\int_0^{\infty} f(t) \mathrm{e}^{-x t^2}\cos(yt^2)\, \mathrm{d}t , \end{equation*}" title="Rendered by QuickLaTeX.com"/><a name="id248469892"></a> (6) <img src="https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-c525384cb6257b3b19256d74df828ee9_l3.png" height="41" width="273" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{equation*} F_s(x,y)=\int_0^{\infty} f(t) \mathrm{e}^{-x t^2}\sin(yt^2)\, \mathrm{d}t . \end{equation*}" title="Rendered by QuickLaTeX.com"/> We arrive at two new real-valued integrals,$

F_c(x,y) $and$ F_s(x,y) $, from the given known integral \eqref{integ}. Given$ F(z)

$they can be integrated readily, <a name="id3033009595"></a> (7) <img src="https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-ff21c624abd2c598f18f4d234424dccc_l3.png" height="36" width="285" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{equation*} F_c(x,y)=\frac{1}{2}(F(x+iy)+F(x-iy)), \end{equation*}" title="Rendered by QuickLaTeX.com"/><a name="id2541638044"></a> (8) <img src="https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-48008d2eb0fa36311ab3442a08aa03b0_l3.png" height="36" width="291" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{equation*} F_s(x,y)=\frac{1}{2 i}(F(x+iy)-F(x-iy)) . \end{equation*}" title="Rendered by QuickLaTeX.com"/>Notice now that these integrals are defined only for positive (real)$

x $and for real$ y $. We ask Can we use the right hand sides of equations \eqref{eq1} and \eqref{eq2} to evaluate the integrals$ F_c $and$ F_s $for some complex values of$ x $and$ y $? Let us consider for the moment the integral$ F_c(x,y) $. Let us fix$ y $and replace the real variable$ x $in$ F_c(x,y) $with the complex number$ \sigma

$. This yields the complex valued function (9) <img src="https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-dc45f44b60ee0d55ce49664f780a7816_l3.png" height="41" width="275" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{equation*} \tilde{F}_c(\sigma,y)=\int_0^{\infty} f(t) \mathrm{e}^{-\sigma t^2} \cos(yt^2)\, \mathrm{d}t . \end{equation*}" title="Rendered by QuickLaTeX.com"/>The integral is absolutely convergent for all$

\sigma $with$ \mathrm{Re}(\sigma)>0 $, so that$ \tilde{F}_c(\sigma,y) $is analytic in the right-half of the complex plane. The functions$ F_c(x,y) $and$ \tilde{F}_c(\sigma,y) $are equal for real$ \sigma $. The complex valued function$ \tilde{F}_c(\sigma,y) $is then the complex extension of the real valued$ F_c(x,y)

$in the complex plane. Moreover, let us define the complex valued function (10) <img src="https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-06bcb5d1bad8d6c1dcd6bcc80c1694bb_l3.png" height="36" width="287" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{equation*} \tilde{F}_c'(\sigma,y)=\frac{1}{2}(F(\sigma+iy)+F(\sigma-iy)), \end{equation*}" title="Rendered by QuickLaTeX.com"/>whic is also analytic for complex$

\sigma $with$ \mathrm{Re}(\sigma)>0 $. This function is the complex extension of the real valued function in the right hand side of equation \eqref{eq1}. The functions$ \tilde{F}_c(\sigma,y) $and$ \tilde{F}_c'(\sigma,y) $have the same domains. Are$ \tilde{F}_c(\sigma,y) $and$ \tilde{F}_c'(\sigma,y) $equal? We know that both functions are equal for all real$ \sigma>0 $. Since both functions are analytic and coincide in a segment contained in their common domain, analytic extension theory asserts that they are everywhere equal in the right-half complex plane, i.e.$ \tilde{F}_c(\sigma,y)=\tilde{F}_c'(\sigma,y) $for all$ \sigma $with$ \mathrm{Re}(\sigma)>0 $for fix real$ y

$. Then we arrive at the integral <a name="id337304938"></a> (11) <img src="https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-8263d8cbea666b0bb4468bc6704f38d8_l3.png" height="41" width="409" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{equation*} \int_0^{\infty}\!\! f(t) \mathrm{e}^{-\sigma t^2}\cos(yt^2)\, \mathrm{d}t = \frac{1}{2}(F(\sigma+iy)+F(\sigma-iy)), \end{equation*}" title="Rendered by QuickLaTeX.com"/> for all$

\sigma $with$ \mathrm{Re}(\sigma)>0 $and$ y\in \mathbb{R}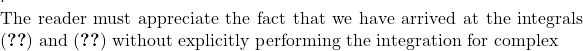 $. Similar consideration for the real-valued function$ F_s(x,y)

$leads us to the other integral identity <a name="id583144588"></a> (12) <img src="https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-7c9d8d2ba6d4ab8861768eb546e12c5c_l3.png" height="41" width="413" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{equation*} \int_0^{\infty}\!\! f(t) \mathrm{e}^{-\sigma t^2}\sin(yt^2)\, \mathrm{d}t = \frac{1}{2 i}(F(\sigma+iy)-F(\sigma-iy)), \end{equation*}" title="Rendered by QuickLaTeX.com"/>also for all$

\sigma $with$ \mathrm{Re}(\sigma)>0 $and$ y\in \mathbb{R} $. The reader must appreciate the fact that we have arrived at the integrals \eqref{be1} and \eqref{be2} without explicitly performing the integration for complex$ \sigma $. It was enough to evaluate the integrals for real$ \sigma $s, and analytically continue the resulting real integrals in the complex plane to obtain the desired complex integrals. I invite the reader to do similar analytic extension analysis of the couple of integrals \eqref{be1} and \eqref{be2} for fixed complex$ \sigma $and for complex$ y

$. For definiteness, you may apply analytic extension to obtain the integrals (13) <img src="https://quant-math.org/wp/wp-content/ql-cache/quicklatex.com-60c2f726f7f5f3986d98453404bc6bb2_l3.png" height="41" width="332" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{equation*} \int_0^{\infty} \cos(\gamma t^2) \mathrm{e}^{- \sigma t^2 }\, \mathrm{d}t, \;\;\; \int_0^{\infty} \sin(\gamma t^2) \mathrm{e}^{- \sigma t^2 }\, \mathrm{d}t \nonumber \end{equation*}" title="Rendered by QuickLaTeX.com"/>for some complex$

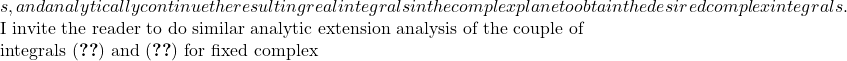\gamma $and$ \sigma$, given the known integral

(14) $\begin{equation*} \int_0^{\infty} \mathrm{e}^{-\sigma t^2} \, \mbox{d}t=\frac{1}{2} \sqrt{\frac{\pi}{\sigma}},\;\;\; \mbox{for} \; \mathrm{Re}(\sigma)>0 . \nonumber \end{equation*}$

Finally, analytic extension theory offers a powerful way of solving problems which take the complex plane as its domain. We have seen that it is possible to reduce the problem to a segment in the relevant domain and then obtain the full solution by analytic extension.

Leave a Reply Cancel reply