How long does it take for a message to be delivered? Everyday experience tells us that in order for a message to arrive quicker, we just need a faster messenger. Considering special relativity and quantum mechanics, however, introduces further complications. If we consider the message to be carried by particles, special relativity imposes a minimum on the arrival time of the particles and quantum mechanics introduces uncertainties to that arrival time. We wish to consider the regime where both these effects are significant. Before we move on, let us first elaborate how these two regimes modify our everyday notion of arrival time.
Special relativity tells us that for any inertial reference frame, light (and in general, any massless particle) travels with the same speed. That is, if you can consider your frame as an inertial reference frame and you measure the speed of light to be some value, then any other frame moving with a constant velocity with respect to you would measure the speed of light to be of the same value. A consequence of the invariance of the speed of light is that no information can be transmitted faster than those carried by light. This is because no matter how fast the particles carrying the information are, they will always observe light rays moving away from them with the same speed just as when they were not moving. The particles can never catch up with light. This seems counter-intuitive since we can always imagine pushing something to make it move faster. However, we would need an infinite amount of energy and momentum for a particle with mass to reach the speed of light. Only massless particles travel with that speed. We don’t notice this relativistic speed limit since we are all moving very slowly as compared to the speed of light. At greater and greater speeds, these effects become more apparent. Thus, when someone from afar is sending messages to us, we would always have to wait a certain amount of time before it can reach us. There is then no instantaneous transmission. That is, its time of arrival is always non-zero. The shortest of which is when they use massless particles (like light) to carry their messages.
Quantum mechanics, on the other hand, tells us that particles are also waves, and waves are also particles. A particle then may not be just a geometric point, but it is also a wave, an entity that is spread out in space. That is, the particle may not have a definite location because its wave-like property introduces uncertainties in its location. This is also true for every physical property of the particle, like its momentum and energy. What we get are the probabilities of these physical quantities to take certain values. Because of its uncertainty in momentum, for example, a free particle may be considered as being more probable to move to the right than to the left. So if we have a collection of identical particles, all of which are described by the same probabilities as stated above, then there would be more particles moving to the right than to the left. These quantum uncertainties seem foreign to us as macroscopic beings since they are so small so that they are practically negligible. However, in the microscopic realm, these quantum uncertainties become most apparent and certainty is replaced with probabilities. Thus, when someone is using particles to carry the ‘letters’ of the message, the arrival times of the particles is uncertain so that the message will arrive in parts. If perhaps there is a small probability for the particles to arrive earlier, then there will be small chunks of the message arriving earlier. And if the most probable time of arrival of the particles is later, then the biggest chunk of the message will arrive later.
What happens then when we combine these two regimes? Consider now our message as being carried by a collection of free particles incident towards a detector and all of the particles have the same average position and the same average momentum. At what time will they reach the detector? As stated before, the particle arrival times will be uncertain and the corresponding probabilities can be calculated. To be more precise, these time of arrival probabilities are derived from a mathematical object called a quantum mechanical operator. Traditionally, the recipe of quantum mechanics to construct these operators is to take a physical quantity (say, the arrival time of particles) described by classical mechanics and use a prescribed ‘canonical quantization rule’ to get the (time of arrival) operator. If, however, we think of classical mechanics (our everyday experience) as just a limiting case of quantum mechanics, this quantization rule seems inappropriate since it appears to imply that quantum mechanical objects can be derived only from classical objects. We should then be able to construct operators from quantum mechanical first principles. For the more advanced reader, we should be able to construct our time of arrival operator from its canonical conjugacy relation with the system Hamiltonian describing a relativistic particle. For more information on the derivation of the said time of arrival operator and the subsequent construction of time of arrival probabilities, please refer to the following links:
http://www.sciencedirect.com/science/article/pii/S0003491614003169
http://www.sciencedirect.com/science/article/pii/S000349161500113X
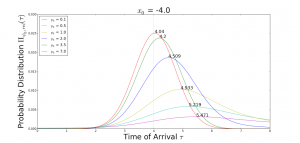
Figure 1: Time of arrival probabilities of a particle starting at the average position x0 for different average momenta p0.
Specifically, Figure 1 shows the probabilities that a particle starting at some average location x0 with some average momentum p0 will arrive at a certain time. Considering a collection of particles with the same x0 and p0 (and the same uncertainties), the majority of the particles in the collection would then arrive at the most probable time. That is, the time corresponding to the curve peaks. It is then seen that even if the average momentum of the particles are increased, the most probable time of arrival is always greater than a certain value. That is the smallest time imposed by special relativity – the time of arrival of light if it had started at the same position x0 (the dotted vertical line). What do the uncertainties in the time of arrival mean then? In the plot, the curves pass through the dotted vertical line. This suggests that there is still a non-zero probability that a particle can arrive at a time before light. Does this mean that we can transmit information faster? It is true that there may be particles that can arrive before light but would they carry enough information? Imagine again that each particle carries a letter from the message sent. Some of the letters may arrive before those carried by light, but that is not the entire message. We would have to wait longer in order for the message to be completed (or at least enough to be deciphered). As can be seen from the figure, the most probable arrival time of the particles, and thus the arrival of the biggest chunk of the information, is later than that of light. The information then is not transmitted faster than that of light. Thus, quantum mechanics does not violate special relativity in this regard. To deliver a message, the fastest way is still to use light.
Post Script
By Eric A. Galapon

By the way Joseph will be earning his PhD in a few months. He will soon be out of my supervisorship and he is actively seeking a post-doctoral position elsewhere. He will be leaving behind a cache of problems in the Hilbert space properties of time operators. Joseph has a knack of doing difficult mathematics, and we will surely miss his math skills. If you have the aptitude to take on tough math problems, contact us if you are interested in picking up where Joseph will leave off.
Check out Joseph’s publications:
- J. Bunao and E.A. Galapon, “A relativistic one-particle Time of Arrival operator for a free spin-1/2 particle in (1+1) dimensions”, Ann. Phys. 356 369–382 (2015).
- J. Bunao and E.A. Galapon, “A one-particle time of arrival operator for a free relativistic spin-0 charged particle in (1+1) dimensions”, Ann. Phys. 353 83–106 (2015).
- J. Bunao and E.A. Galapon, “The Bender-Dunne basis operators as Hilbert space operators”, J. Math. Phys. 55, 022102 (2014).